Généralités sur les réacteurs idéaux
Définition : Réacteurs idéaux
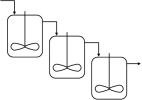
Les réacteurs dits idéaux sont au nombre de trois :
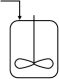
le réacteur fermé (batch reactor) : Son idéalité tient dans le fait que les grandeurs qui le caractérisent (composition, température, etc.) sont uniformes. Il fonctionne en discontinu.
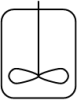
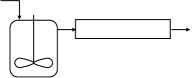
le réacteur parfaitement agité - RPA (constant flow stirred tank reactor - CFSTR) : C'est la version continue du précédent. Ainsi non seulement les grandeurs qui le caractérisent sont uniformes, mais elles sont en outre constantes dans le temps (régime permanent).
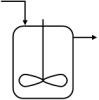
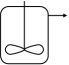
le réacteur piston (plug flow reactor) : Il fonctionne lui aussi en régime permanent ; mais contrairement au précédent, les tranches de fluide y entrent successivement et y progressent les unes derrière les autres sans se mélanger.

Rappel : Bilan de matière global
Le bilan de matière global sur un système quelconque s'écrit en terme de débits (flux) massiques[1] :
\(Q_m^e\) et \(Q_m^s\) sont respectivement les débits massiques[1] totaux entrant et sortant du système ; \(\frac{\mathrm{d} m}{\mathrm{d} t}\) est le terme d'accumulation de masse totale.
En régime permanent, il n'y a pas de terme d'accumulation. Pour un système fermé, il n'y a pas de termes d'entrée ni de sortie.
Notion fondamentale : Écriture du bilan en une espèce dans les réacteurs
Le bilan en espèce \(j\) sur un système réactif quelconque s'écrit en terme de débits (flux) molaires[2] : \(F_j^e + F_j^{production} = F_j^s + \frac{\mathrm{d} n_j}{\mathrm{d} t}\)
\(F_j^e\) et \(F_j^s\) sont respectivement les débits molaires d'espèce \(j\) entrant et sortant du système ; \(F_j^{production}\) est le terme de production de \(j\) par les différentes réactions ; \(\frac{\mathrm{d} n_j}{\mathrm{d} t}\) est le terme d'accumulation de l'espèce \(j\).
Le mot "production" s'entend ici au sens large : il peut s'agir d'une production comme produit d'une ou plusieurs réaction(s) chimique(s) ou au contraire d'une consommation (production négative) en tant que réactif d'une ou plusieurs réaction(s). De sorte que :
\(F_j^{production} = {{\left. \frac{\mathrm{d} n_j}{\mathrm{d} t} \right|}_{r\acute{e}actions}} = \mathcal{R}_j \cdot V\) comme on l'a vu au chapitre précédent.
D'où le bilan en espèce \(j\) sur un réacteur :
Attention : Système sur lequel on peut écrire ce bilan
La vitesse de réaction dépendant de la composition du mélange et de sa température, ce bilan ne peut s'écrire ainsi que sur un volume dont la composition et la température sont uniformes.
Remarque : Expression des concentrations
Les lois de vitesse s'exprimant le plus souvent en fonction de concentrations[3], il faut relier ces dernières aux nombres de moles ou aux flux molaires :
en réacteur fermé uniforme : \(C_j = \frac{n_j}{V}\)
en réacteur ouvert en régime permanent : \(C_j = \frac{F_j}{Q_v}\)
Les expressions de \(V\) et \(Q_v\) ont été vues précédemment ou sont à retrouver à partir des équations d'état (loi des gaz parfaits ou autre).