Quantification du rendement et de la sélectivité
En présence de réactions parasites, la notion de taux de conversion[1] ou d'avancement[2] n'est plus suffisante pour mesurer l'efficacité du réacteur pour fabriquer le produit d'intérêt. On doit alors définir d'autres grandeurs.
Impossible d'accéder à la ressource audio ou vidéo à l'adresse :
La ressource n'est plus disponible ou vous n'êtes pas autorisé à y accéder. Veuillez vérifier votre accès puis recharger le média.
Rendements
Définition : rendement global
Dans les réacteurs ouverts, on définit le rendement global[4] (également appelé taux de produit utile) :
\(Y_{P/A} = \frac{F_P}{\nu_{P/A} \cdot F_{A0}}\)
où P est le produit désiré, A le réactif clé et \(\nu_{P/A}\) le nombre maximum de moles de P que l'on peut obtenir à partir d'une mole de A
\(Y_{P/A}\) est toujours inférieur à 1, car d'autres réactions peuvent consommer A et tout A n'est pas converti.
Définition : rendement relatif global
On peut également définir un rendement relatif global[5] :
\(\eta_{P/A} = \frac{Y_{P/A}}{1 - X_A} = \frac{F_P}{\nu_{P/A} \cdot \left( F_{A0} - F_A \right)}\)
Définition : rendement relatif local
Enfin on définit un rendement relatif local[6] :
\(\eta'_{P/A} = \frac{\mathcal{R}_P}{\nu_{P/A} \cdot \left( - \mathcal{R}_A \right)}\) toujours positif
Méthode :
Dans le cas d'un réacteur fermé, on remplace dans toutes ces définitions les flux molaires par des nombres de moles.
Remarque : Le rendement relatif local est la dérivée du rendement global.
D'après la définition du rendement global, par dérivation, il vient : \(\mathrm{d}Y_{P/A} = \frac{\mathrm{d}F_P}{\nu_{P/A} \cdot F_{A0}}\).
Par ailleurs \(X_A = 1 - \frac{F_A}{F_{A0}}\), donc, toujours par dérivation, il vient : \(\mathrm{d}X_A = -\frac{\mathrm{d}F_A}{F_{A0}}\). Ainsi, en divisant les 2 expressions, on a : \(\frac{\mathrm{d}Y_{P/A}}{\mathrm{d}X_A} = -\frac{\mathrm{d}F_P}{\nu_{P/A} \cdot \mathrm{d}F_A}\).
Or par définition (cf. rappels de cinétique au chapitre I), \(\mathcal{R}_A = -\frac{1}{V} \cdot {\left. \frac{\mathrm{d}n_A}{\mathrm{d}t} \right|}_{r\acute{e}actions}\) et \(\mathcal{R}_P = \frac{1}{V} \cdot {\left. \frac{\mathrm{d}n_P}{\mathrm{d}t} \right|}_{r\acute{e}actions}\), donc \(\frac{\mathcal{R}_P}{- \mathcal{R}_A} = \frac{\mathrm{d}n_P}{\mathrm{d}n_A} = \frac{\mathrm{d}F_P}{\mathrm{d}F_A}\), c'est-à-dire \(\eta'_{P/A} = \frac{\mathrm{d}F_P}{\nu_{P/A} \cdot \mathrm{d}F_A}\) (pour qu'il soit positif), qui se trouve donc être égal à \(\frac{\mathrm{d}Y_{P/A}}{\mathrm{d}X_A}\).
C'est pour cette raison que le rendement relatif local est aussi appelé rendement différentiel.
Notion fondamentale : Optimisation du rendement global
Le rendement global s'obtient donc par intégration du rendement relatif local.
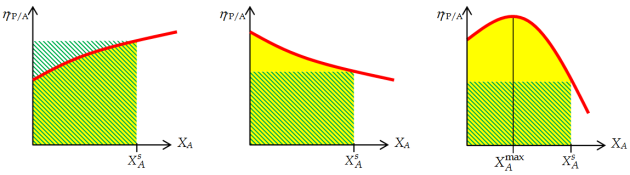
Le rendement global d'un RPA fonctionnant en régime permanent est ainsi égal à l'aire du rectangle hachuré en vert sur les graphiques suivants (courbes \(\eta'_{P/A}\) vs \(X_A\)), puisque le taux de conversion et le rendement relatif local sont uniformes dans le RPA, égaux à leurs valeurs en sortie du réacteur.
Tandis que le rendement global d'un réacteur piston fonctionnant en régime permanent est égal à l'aire sous la courbe, coloriée en jaune sur les graphiques suivants.
On remarque sur les graphiques précédents que :
lorsque la courbe \(\eta'_{P/A}\) vs \(X_A\) est monotone croissante, le réacteur piston aura toujours un rendement global inférieur au RPA continu permettant d'obtenir le même taux de conversion en sortie ;
lorsque cette courbe est monotone décroissante, c'est le réacteur piston qui aura le meilleur rendement global, pour un taux de conversion en sortie donné ;
lorsque cette courbe présente un maximum, il n'y a pas de réponse unique : tout dépend de la forme de la courbe et de la position de ce maximum.
Les tendances sont donc inversées par rapport au Levenspiel plot. Et contrairement au cas de l'optimisation du volume du réacteur, la forme de la courbe est difficilement prévisible, en plus d'être très variable d'une situation à l'autre.
Il est par conséquent délicat de dégager des règles quant au choix du meilleur réacteur dans le cas de plusieurs réactions ; le chapitre consacré à ces cas de figure dans l' ouvrage d'Octave LEVENSPIEL[8] s'appelle d'ailleurs Potpourri of Mutiple Reactions. Nous verrons donc des exemples afin de dégager une méthode d'étude.
Sélectivité
La sélectivité[9] compare les productions de deux produits P1 et P2 à partir d'un même réactif clé A :
\(s_{P1/P2} = \frac{\nu_{P2/A}}{\nu_{P1/A}} \cdot \frac{n_{P1}}{n_{P2}}\) en réacteur fermé
\(s_{P1/P2} = \frac{\nu_{P2/A}}{\nu_{P1/A}} \cdot \frac{F_{P1}}{F_{P2}}\) en réacteur ouvert