Conclusion générale
Impossible d'accéder à la ressource audio ou vidéo à l'adresse :
La ressource n'est plus disponible ou vous n'êtes pas autorisé à y accéder. Veuillez vérifier votre accès puis recharger le média.
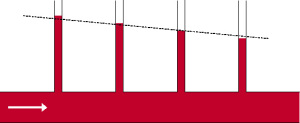
En régime permanent, pour un fluide incompressible dans le champ de pesanteur seul, on a donc :
Au repos, le principe fondamental de l'hydrostatique :
\(P_1 + \rho \cdot g\cdot z_1 = P_2 + \rho \cdot g \cdot z_2\)

Pour un fluide parfait[3] en écoulement, l'équation de Bernoulli :
\(P_1 + \rho \cdot g \cdot z_1 + \frac{\rho \cdot {u_1}^2}{2} = P_2 + \rho \cdot g \cdot z_2 + \frac{\rho \cdot {u_2}^2}{2}\)
Cette équation correspond au principe fondamental de l'hydrostatique auquel on aurait ajouté les termes d'énergie cinétique liés au mouvement.
Pour un fluide réel en écoulement, l'équation de Bernoulli comporte un terme de plus \(\Delta P_{fr}\) traduisant les pertes de charge régulières dues aux frottements au sein du fluide non-parfait et contre les parois :
\(P_1 + \rho \cdot g \cdot z_1 + \frac{\rho \cdot {u_1}^2}{2} = P_2 + \rho \cdot g \cdot z_2 + \frac{\rho \cdot {u_2}^2}{2} + \Delta{P_{fr}}\)
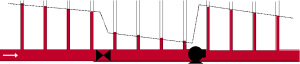
Pour un fluide réel, en présence de singularités et d'une pompe, l'équation de Bernoulli généralisée :
\(P_1 + \rho \cdot g \cdot z_1 + \frac{\rho \cdot {u_1}^2}{2} + \Delta P_{pompe} = P_2 + \rho \cdot g \cdot z_2 + \frac{\rho \cdot {u_2}^2}{2} + \Delta{P_f}\)
C'est l'équation de Bernoulli avec un terme source d'énergie lié à la pompe (dans le membre de gauche) et un terme de dissipation d'énergie dues aux frottements du fluide réel et aux singularités (dans le membre de droite).
Ce terme de perte de charge est détaillé sous la forme :
\(\Delta{P_f} = \Delta{P_{fr}} + \sum{\Delta{P_{fs}}} = \frac{\rho \cdot {u^2}}{2} \cdot \left( 8 \cdot f/2 \cdot \frac{L}{D} + \sum{k} \right)\)