Comparaison des réacteurs idéaux
Impossible d'accéder à la ressource audio ou vidéo à l'adresse :
La ressource n'est plus disponible ou vous n'êtes pas autorisé à y accéder. Veuillez vérifier votre accès puis recharger le média.
Raisonnement :
On peut déduire un comparatif qualitatif (voire quantitatif) entre réacteurs idéaux à partir du cas particulier des bilans à volume (ou débit volumique) constant avec un coefficient stœchiométrique du réactif clé A égal à -1. Pour cela reprenons les expressions des bilans de matière dans les différents cas :
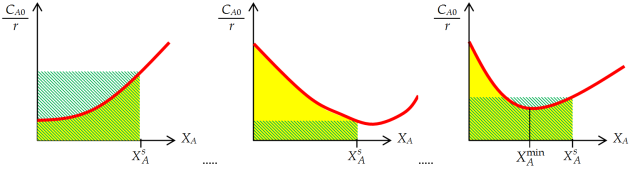
réacteur parfaitement agité (continu, en régime permanent) : \(F_{A0} - r \cdot V = F_{A0} \cdot \left( 1 - X_A^s \right)\), soit \(r \cdot V = F_{A0} \cdot X_A^s\), qui à débit volumique contant devient \(r \cdot \tau = C_{A0} \cdot X_A^s\) (on a divisé chaque membre par \(Q_v\)), que l'on peut réarranger en \(\tau = \frac{C_{A0}}{r} \cdot X_A^s\) ; comme un RPA fonctionne dans les conditions de sortie, on peut aussi écrire \(\tau =\left. \frac{C_{A0}}{r} \right|_s \cdot X_A^s\) ; ainsi le temps de passage[2] dans le RPA continu est l'aire du rectangle de base \(X_A^s\) et de hauteur \(\left. \frac{C_{A0}}{r} \right|_s\) figuré en vert sur les graphiques suivants (appelés Levenspiel plot) ;
réacteur piston (en régime permanent) : \(- r \cdot \mathrm{d}V = \mathrm{d}F_A = - F_{A0} \cdot \mathrm{d}X_A\), qui à débit volumique contant devient \(r \cdot \mathrm{d}\tau = C_{A0} \cdot \mathrm{d}X_A\), que l'on peut intégrer en \(\tau = \int\limits_{0}^{X_A^s}{\frac{C_{A0}}{r} \cdot \mathrm{d} X_A}\) ; ainsi le temps de passage dans le réacteur piston est l'aire jaune sous la courbe rouge sur les graphiques suivants ;
réacteur fermé (parfaitement agité) : \(- r \cdot V = \frac{\mathrm{d} n_A}{\mathrm{d} t}\), qui à volume contant devient \(- r = \frac{\mathrm{d} C_A}{\mathrm{d} t} = - C_{A0} \cdot \frac{\mathrm{d} X_A}{\mathrm{d} t}\), que l'on peut intégrer en \(t = \int\limits_{0}^{X_A^s}{\frac{C_{A0}}{r} \cdot \mathrm{d} X_A}\) ; on retrouve l'équivalence entre temps de passage dans le réacteur piston et temps de fonctionnement du RPA fermé déjà évoqué précédemment.
Notion fondamentale : Levenspiel plot
Le temps de passage dans un RPA fonctionnant en régime permanent est égal à l'aire du rectangle hachuré en vert sur le Levenspiel plot (courbe \(\frac{C_{A0}}{r}\) vs \(X_A\)). Tandis que le temps de passage dans un réacteur piston fonctionnant en régime permanent (mais aussi le temps de fonctionnement d'un RPA fermé) est égal à l'aire sous la courbe, coloriée en jaune sur les graphiques suivants.
Remarque : Plus petit réacteur
On remarque sur les graphiques précédents que :
lorsque la courbe \(\frac{C_{A0}}{r}\) vs \(X_A\) est monotone croissante (cas le plus courant), le réacteur piston aura toujours un temps de passage (et donc un volume, à débit volumique fixé) inférieur au RPA continu permettant d'obtenir le même taux de conversion en sortie ;
lorsque cette courbe présente un minimum et que le taux de conversion recherché se trouve avant ce minimum (ce qui revient à une zone où la courbe est monotone décroissante), c'est le RPA continu qui aura le plus petit volume, pour un taux de conversion en sortie donné ;
lorsque cette courbe présente un minimum situé avant le taux de conversion recherché, il n'y a pas de réponse unique : tout dépend de la forme de la courbe et de la position du minimum par rapport au taux de conversion en sortie souhaité.
Cette différence se comprend aisément lorsque l'on songe à la manière de fonctionner d'un réacteur piston par rapport à un réacteur parfaitement agité continu :
le RPA fonctionnant dans les conditions de sortie, il y règne une concentration en réactif(s) uniforme et faible ; si la loi de vitesse dépend uniquement de concentrations de réactifs (la courbe \(\frac{C_{A0}}{r}\) vs \(X_A\) est alors monotone croissante), la vitesse de réaction partout dans le RPA sera faible et il faudra un réacteur de grande taille pour atteindre le taux de conversion en sortie voulu ;
alors que dans un réacteur piston, la concentration en réactif(s) est grande en entrée, puis diminue progressivement ; la vitesse de réaction, toujours lorsqu'elle dépend uniquement des concentrations des réactifs, est donc grande en entrée et diminue jusqu'à la sortie ; il faut par conséquent un réacteur de plus petit taille pour obtenir le même taux de conversion en sortie que dans le RPA continu ;
dans un RPA fermé, la concentration en réactif(s) est certes uniforme, mais elle évolue dans le temps : elle est grande au début de l'opération, puis diminue au cours de la fabrication ; le phénomène est encore une fois similaire à ce qui se produit dans le réacteur piston.