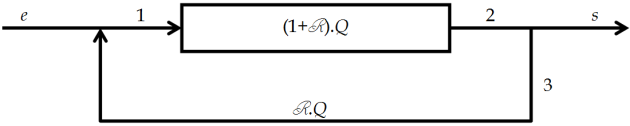
Réacteur piston avec recyclage optimal
Une substance A se transforme selon la réaction autocatalytique d'ordre global 2 : A → R (ΔrH° = -10 kJ/kg) ; cette réaction est mise en œuvre en phase liquide, sans variation de volume. La constante de vitesse est égale à 1 L mol-1 min-1. On veut traiter un débit d'alimentation FA0 = 1 mol min-1 contenant seulement A (CA0 = 1 mol L-1, CR0 = 0) à la température de 25°C, dans un réacteur piston avec recyclage. On veut obtenir 99% de conversion.
Question
Trouver le taux de recyclage Ropt qui minimise le volume du réacteur nécessaire. Calculer le volume Vopt correspondant.
Indice
Définir le taux de conversion, puis établir les relations entre les débits et les compositions aux niveaux du diviseur de courant en sortie de réacteur et de la jonction en entrée, enfin écrire le bilan en A sur le réacteur.
Indice
En manipulant les différentes équations obtenues, établir l'expression du volume du réacteur en fonction du taux de recyclage. Il "suffira" alors de trouver (graphiquement) quel taux de recyclage minimise ce volume.
Résultat
Il s'agit de trouver le minimum du volume, dont l'expression en fonction du taux de recyclage \(R\) est \(V = \frac{\left( 1+R \right) \cdot F_{A0}}{k \cdot C_{A0}^2} \cdot \ln \ \left[ \frac{1}{R \cdot \left( 1 - X_A^s \right)} +1 \right]\) : Ropt = 0,189 ; ce qui correspond à Vopt = 7,46 L
Solution détaillée
définition du taux de conversion : \({{F}_{As}}={{F}_{Ae}}\cdot \left( 1-X_{A}^{s} \right)={{F}_{A0}}\cdot \left( 1-X_{A}^{s} \right)\)
D'une part le débit volumique DANS le réacteur est (1+R).Q et il vaut Q à la sortie (s), d'autre part la composition des flux 2, 3 et s est la même (diviseur de courants), le taux de conversion X DANS le réacteur est donc tel que : \({{F}_{A}}={{F}_{A0}}\cdot \left( 1+R \right)\cdot \left( 1-{{X}_{A}} \right)\).
bilans aux nœuds : \({{F}_{A1}}={{F}_{Ae}}+{{F}_{A3}}={{F}_{A0}}+R\cdot {{F}_{As}}={{F}_{A0}}\cdot \left[ 1+R\cdot \left( 1-X_{A}^{s} \right) \right]\)
\({{F}_{A2}}={{F}_{As}}+{{F}_{A3}}=\left( 1+R \right)\cdot {{F}_{As}}={{F}_{A0}}\cdot \left( 1+R \right)\cdot \left( 1-X_{A}^{s} \right)\)
Dans le réacteur, \({{F}_{A}}={{F}_{A0}}\cdot \left( 1+R \right)\cdot \left( 1-{{X}_{A}} \right)\), donc à l'entrée du réacteur : \({{F}_{A1}}={{F}_{A0}}\cdot \left( 1+R \right)\cdot \left( 1-X_{A}^{1} \right)\)
D'où, \({{F}_{A0}}\cdot \left[ 1+R\cdot \left( 1-X_{A}^{s} \right) \right]={{F}_{A1}}={{F}_{A0}}\cdot \left( 1+R \right)\cdot \left( 1-X_{A}^{1} \right)\).
Par conséquent, \(X_{A}^{1}=1-\frac{1+R\cdot \left( 1-X_{A}^{s} \right)}{1+R}=\frac{1+R-1-R+R\cdot X_{A}^{s}}{1+R}\), soit \(X_{A}^{1}=\frac{R}{1+R}\cdot X_{A}^{s}\)
bilan en A sur le réacteur : \(d{{F}_{A}}=-r\cdot dV\), soit \({{F}_{A0}}\cdot \left( 1+R \right)\cdot d{{X}_{A}}=k\cdot {{C}_{A}}\cdot {{C}_{R}}\cdot dV\)
Or \({{C}_{A}}=\frac{{{F}_{A}}}{\left( 1+R \right)\cdot Q}$ et ${{C}_{R}}=\frac{{{F}_{R}}}{\left( 1+R \right)\cdot Q}\)
Avec \({{F}_{A}}={{F}_{A0}}\cdot \left( 1+R \right)\cdot \left( 1-{{X}_{A}} \right)\) et \({{F}_{R}}=\left( 1+R \right)\cdot \left( {{F}_{Re}}+{{F}_{Ae}}\cdot {{X}_{A}} \right)=\left( 1+R \right)\cdot {{F}_{A0}}\cdot {{X}_{A}}\)
Comme \(Q=\frac{{{F}_{A0}}}{{{C}_{A0}}}\) et FR0 = 0, \({{C}_{A}}={{C}_{A0}}\cdot \left( 1-{{X}_{A}} \right)\) et \({{C}_{R}}={{C}_{A0}}\cdot {{X}_{A}}\)
Le bilan s'écrit donc : \({{F}_{A0}}\cdot \left( 1+R \right)\cdot d{{X}_{A}}=k\cdot {{C}_{A0}}^{2}\cdot \left( 1-{{X}_{A}} \right)\cdot {{X}_{A}}\cdot dV\)
On intègre : \(\int\limits_{X_{A}^{1}}^{X_{A}^{s}}{\frac{dX}{\left( 1-{{X}_{A}} \right)\cdot {{X}_{A}}}}=\int\limits_{X_{A}^{1}}^{X_{A}^{s}}{\frac{dX}{1-{{X}_{A}}}}+\int\limits_{X_{A}^{1}}^{X_{A}^{s}}{\frac{dX}{{{X}_{A}}}}=\frac{k\cdot {{C}_{A0}}^{2}}{\left( 1+R \right)\cdot {{F}_{A0}}}\cdot \int\limits_{0}^{V}{dV}\)
D'où : \(\left[ -\ln \ \left( 1-{{X}_{A}} \right) \right]_{X_{A}^{1}}^{X_{A}^{s}}+\left[ \ln \ \left( {{X}_{A}} \right) \right]_{X_{A}^{1}}^{X_{A}^{s}}=\frac{k\cdot {{C}_{A0}}^{2}}{\left( 1+R \right)\cdot {{F}_{A0}}}\cdot V\)
Soit \(\begin{align}& \frac{k\cdot {{C}_{A0}}^{2}}{\left( 1+R \right)\cdot {{F}_{A0}}}\cdot V=\ln \frac{X_{A}^{s}}{1-X_{A}^{s}}-\ln \frac{X_{A}^{1}}{1-X_{A}^{1}}=\ln \frac{X_{A}^{s}}{1-X_{A}^{s}}-\ln \frac{\frac{R}{1+R}\cdot X_{A}^{s}}{1-\frac{R}{1+R}\cdot X_{A}^{s}} \\& =\ln \frac{X_{A}^{s}}{1-X_{A}^{s}}-\ln \frac{R\cdot X_{A}^{s}}{1+R-R\cdot X_{A}^{s}}=\ln \frac{X_{A}^{s}\cdot \left( 1+R-R\cdot X_{A}^{s} \right)}{\left( 1-X_{A}^{s} \right)\cdot R\cdot X_{A}^{s}}=\ln \frac{1+R-R\cdot X_{A}^{s}}{R\cdot \left( 1-X_{A}^{s} \right)}\end{align}\)
Finalement, \(V = \frac{\left( 1+R \right) \cdot F_{A0}}{k \cdot C_{A0}^2} \cdot \ln \ \frac{1 + R - R \cdot X_A^s}{R \cdot \left( 1 - X_A^s \right)} = \frac{\left( 1+R \right) \cdot F_{A0}}{k \cdot C_{A0}^2} \cdot \ln \ \left[ \frac{1}{R \cdot \left( 1 - X_A^s \right)} +1 \right]\)
\(\begin{align}& \frac{dV}{dR}=\frac{{{F}_{A0}}}{k\cdot {{C}_{A0}}^{2}}\cdot \left( \ln \ \left[ \frac{1}{R\cdot \left( 1-X_{A}^{s} \right)}+1 \right]+\left( 1+R \right)\cdot \frac{\frac{-1}{{{R}^{2}}\cdot \left( 1-X_{A}^{s} \right)}}{\frac{1}{R\cdot \left( 1-X_{A}^{s} \right)}+1} \right) \\& =\frac{{{F}_{A0}}}{k\cdot {{C}_{A0}}^{2}}\cdot \left( \ln \ \left[ \frac{1}{R\cdot \left( 1-X_{A}^{s} \right)}+1 \right]-\frac{1+R}{R\cdot \left[ 1+R\cdot \left( 1-X_{A}^{s} \right) \right]} \right)\end{align}\)

On trouve numériquement Ropt tel que : \(\frac{dV}{dR}=0\), soit Ropt = 0,189, ce qui correspond à Vopt = 7,46 L.
Question
Comparer ce volume optimal avec celui qu'il faut prévoir si R = 4.
Solution
Pour R = 4, V = 16,29 L, soit plus de deux fois plus.
Question
Comparer Vopt avec le volume à prévoir pour un réacteur agité (R infini) et pour un réacteur piston sans recyclage (R = 0).
Indice
Pour le RPA on peut soit regarder comment évolue l'équation obtenue à la première question quand R tend vers l'infini, soit écrire le bilan en A sur le RPA.
Indice
Pour le réacteur piston sans recyclage, il faut faire tendre R vers zéro dans l'équation de la première question...
Résultat
Le RPA fera 100 L.
Il est impossible de mener cette production dans un réacteur piston.
Solution détaillée
bilan en A dans un RPA : \({{F}_{A0}}\cdot X_{A}^{s}=k\cdot {{C}_{A0}}^{2}\cdot \left( 1-X_{A}^{s} \right)\cdot X_{A}^{s}\cdot {{V}_{RPA}}\) Donc \({{V}_{RPA}}=\frac{{{F}_{A0}}}{k\cdot {{C}_{A0}}^{2}\cdot \left( 1-X_{A}^{s} \right)}\) = 100 L
On peut retrouver cette expression, en faisant tendre vers l'infini le taux de recyclage R dans l'expression obtenue à la première question : (on rappelle que pour x petit, ln(1+x) est équivalent à x)
Dans un réacteur piston sans recyclage, \(V=\frac{{{F}_{A0}}}{k\cdot {{C}_{A0}}^{2}}\cdot \left( 1+R \right)\cdot \ln \frac{1+R-R\cdot X_{A}^{s}}{R\cdot \left( 1-X_{A}^{s} \right)}\xrightarrow[R\to 0]{}\infty\), ce qui traduit le fait que la réaction autocatalytique ne commence jamais (CR0 = 0).
NB : Dans le réacteur piston avec recyclage, le même problème se pose lors du démarrage de l'installation, ensuite le recyclage apporte le produit R nécessaire à la réaction.