Exploitation qualitative de la DTS : diagnostic des écoulements
Impossible d'accéder à la ressource audio ou vidéo à l'adresse :
La ressource n'est plus disponible ou vous n'êtes pas autorisé à y accéder. Veuillez vérifier votre accès puis recharger le média.
La simple observation de la forme de la courbe \(E\) obtenue permet d'effectuer un diagnostic de l'écoulement.
Notion fondamentale : Les réacteurs idéaux
Il existe deux situations limites d'écoulement :
L'écoulement piston, caractérisé par le fait que tous les éléments situés dans une section droite progressent à la même vitesse, comme poussés par un piston. Le temps de séjour est identique pour tous les éléments et la composition évolue le long du réacteur : on obtient de la sorte un traitement très uniforme de la matière.
Le mélange parfait, qui se traduit par le fait que des propriétés physico-chimiques (concentration, température, etc.) sont les mêmes en tout point du réacteur et identiques à celles de la sortie. Dans le cas d'un fonctionnement continu, le mélange parfait donne lieu à une importante distribution des temps de séjour des éléments : certains quittent le système dès l'introduction (court-circuit), d'autres séjournent très longtemps (par suite de recirculations) ; ainsi les temps de séjour s'échelonnent de zéro à l'infini.
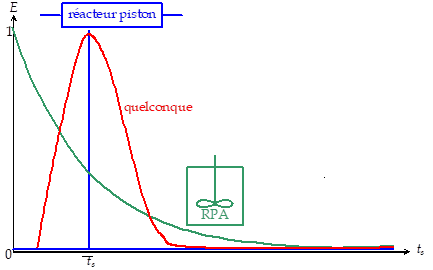
L'intérêt de ces deux concepts simples et extrêmes est que leur fonctionnement est bien connu. Par exemple on sait très bien calculer le taux de conversion chimique dans un réacteur piston ou un réacteur parfaitement agité (RPA).
Remarque :
En l'absence de ces défauts d'écoulement, on a \(E\ \left( t_s \right) = \frac{C\ \left( t_s \right)}{C_0 \cdot \tau}\).
Réacteur piston
Un réacteur piston se comporte comme un retard pur. Toutes les molécules ont le même temps de séjour, c'est le temps de séjour moyen[3], et aussi le temps de passage[4]. La réponse à une impulsion est donc simplement une impulsion décalée dans le temps de \(\overline{t_s}=\tau\) :
\(C\left( t_s \right) = C_0 \cdot \delta \ \left( t_s - \tau \right)\), où la fonction \(\delta\) est la fonction dirac : \(\delta (x) = 1\) pour \(x=0\) ; \(\delta (x) = 0\) pour \(x\ne 0\).
On voit que \(\int\limits_{0}^{\infty}{C\ \left( t_s \right) \cdot \mathrm{d}t_s} = C_0 \cdot \tau\). Ainsi, \(E\ \left( t_s \right) = \frac{\delta \ \left( t_s - \tau \right)}{\tau}\).
Cette fonction distribution des temps de séjour dans un réacteur piston est représentée en bleu sur la figure précédente.
RPA
Dans le cas d'une injection impulsion de \(N\) moles de traceur, le bilan en traceur sur le réacteur parfaitement agité fonctionnant en régime permanent s'écrit :
\(0 = Q_v \cdot C_{traceur} + V \cdot \frac{\mathrm{d}C_{traceur}}{\mathrm{d}t}\)
Avec comme condition initiale la concentration \(C_0 = \frac{N}{V}\), la solution de cette équation différentielle du premier ordre sans second membre est :
\(C = C_0 \cdot \exp \ \left( -\frac{t_s}{\tau} \right)\)
La concentration en traceur croît donc instantanément de 0 à \(C_0\) à l'instant d'injection du traceur, puis décroît exponentiellement. Elle ne devient inférieure à 1% de \(C_0\) qu'au bout de \(5 \cdot \overline{t_s}\).
Notons que le temps de séjour moyen et le temps de passage sont ici aussi égaux : \(\overline{t_s} = \tau = \frac{V}{Q_v}\).
Ainsi, \(E\ \left( t_s \right) = \frac{1}{\tau} \cdot \exp \ \left( -\frac{t_s}{\tau} \right)\).
Cette fonction distribution des temps de séjour dans un RPA est représentée en vert sur la figure précédente.
Raisonnement : Égalité entre temps de séjour moyen et le temps de passage dans un RPA
En effet \(\overline{{{t}_{s}}}={{\mu }_{1}}=\int\limits_{0}^{\infty }{{{t}_{s}}\cdot E\ \left( {{t}_{s}} \right)\cdot d{{t}_{s}}}=\int\limits_{0}^{\infty }{{{t}_{s}}\cdot \frac{C\ ({{t}_{s}})}{\int\limits_{0}^{\infty }{C\ (t)\cdot dt}}\cdot d{{t}_{s}}}=\frac{\int\limits_{0}^{\infty }{{{t}_{s}}\cdot C\ \left( {{t}_{s}} \right)\cdot d{{t}_{s}}}}{\int\limits_{0}^{\infty }{C\ (t)\cdot dt}}=\frac{\int\limits_{0}^{\infty }{{{t}_{s}}\cdot {{C}_{0}}\cdot \exp \ \left( -\frac{{{t}_{s}}}{\tau } \right)\cdot d{{t}_{s}}}}{\int\limits_{0}^{\infty }{{{C}_{0}}\cdot \exp \ \left( -\frac{t}{\tau } \right)\cdot dt}}\)
Or \(\int\limits_{0}^{\infty }{{{C}_{0}}\cdot \exp \ \left( -\frac{t}{\tau } \right)\cdot dt}=\left[ -{{C}_{0}}\cdot \tau \cdot \exp \ \left( -\frac{t}{\tau } \right) \right]_{0}^{\infty }=-{{C}_{0}}\cdot \tau \cdot \left( 0-1 \right)={{C}_{0}}\cdot \tau\).
D'autre part \(\int{x\cdot \exp \ \left( -k\cdot x \right)\cdot dx}=\frac{-1}{k}\cdot x\cdot \exp \ \left( -k\cdot x \right)-\frac{1}{{{k}^{2}}}\cdot \exp \ \left( -k\cdot x \right)\) [ceci s'obtient par intégration par parties].
donc \(\overline{{{t}_{s}}}=\frac{{{C}_{0}}\cdot \left[ -\tau \cdot {{t}_{s}}\cdot \exp \ \left( -\frac{{{t}_{s}}}{\tau } \right)-{{\tau }^{2}}\cdot \exp \ \left( -\frac{{{t}_{s}}}{\tau } \right) \right]_{0}^{\infty }}{{{C}_{0}}\cdot \tau }=-\left[ {{t}_{s}}\cdot \exp \ \left( -\frac{{{t}_{s}}}{\tau } \right)+\tau \cdot \exp \ \left( -\frac{{{t}_{s}}}{\tau } \right) \right]_{0}^{\infty }=-\left[ 0-0+\tau \cdot \left( 0-1 \right) \right]=\tau\)
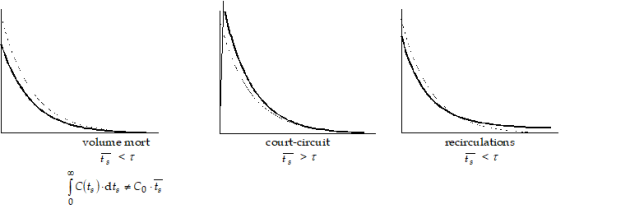
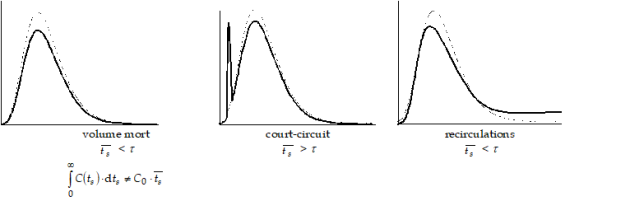
Défauts d'écoulement typiques
Comme on le voit sur cette même figure, un système réel présente un cas intermédiaire entre : d'une part la situation du mélangeur parfait ; d'autre part la situation de l'écoulement piston.
Le temps de séjour moyen \(\overline{t_s}\) et le temps de passage \(\tau = \frac{V}{Q_v}\) calculé à partir du débit volumique d'alimentation \(Q_v\) du système, peuvent être différents ; en outre on peut avoir \(\int\limits_{0}^{\infty}{C\ \left( t_s \right) \cdot \mathrm{d}t_s} \ne C_0 \cdot \overline{t_s} \); en particulier si tout le volume interne n'est pas réellement accessible au fluide.
Ceci est illustré sur les deux figures suivantes.