Utilisation du modèle de Cholette et Cloutier

On effectue dans un réacteur agité fonctionnant en continu en régime permanent la réaction A → P dont la cinétique est du premier ordre et dont la constante de vitesse k a été évaluée à 0,185 min-1 à la température de travail désirée. Cette production de P est obtenue avec une cuve de 4000 L de volume alimentée avec un débit volumique de 3000 L/h d'une solution de réactif A, mais les résultats obtenus en termes de conversion ne correspondent pas à l'estimation initiale obtenue avec l'hypothèse d'une agitation parfaite.

Afin de comprendre ce manque de conversion, on envisage un "essai à blanc" avec un traceur pour mieux cerner l'hydrodynamique de l'installation et préciser la distribution des temps de séjour.

La cuve est remplie d'eau avec un traceur à la concentration CT0 puis, à l'instant t=0, elle est alimentée en eau pure et on mesure l'évolution de la concentration en traceur CT à la sortie de la cuve en fonction du temps t. Les résultats obtenus sont récapitulés dans le tableau suivant :

Résultat des mesures de concentration en traceur en sortie de réacteur

t [min]

CTCT0 [-]

5

0,843

10

0,789

15

0,739

20

0,691

25

0,647

30

0,606

35

0,567

40

0,531

45

0,497

50

0,465

55

0,435

60

0,407

65

0,381

Question

  1. Déterminer l'expression donnant l'évolution de la concentration CT du traceur à la sortie du réacteur si la cuve était parfaitement agitée et comparer les concentrations qui seraient ainsi obtenues aux résultats expérimentaux du tableau précédent.

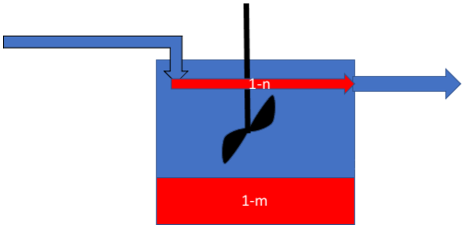
  2. On se propose de modéliser l'hydrodynamique en utilisant un modèle avec court-circuit et volume mort (Modèle de Cholette et Cloutier illustré par la figure suivante) : une fraction (1-n) du débit volumique d'alimentation sort directement de la cuve (courant de court-circuit) et une fraction (1-m) du volume de la cuve est occupée par une quantité de liquide stagnant sans échange de matière avec le restant de l'installation.

    Déterminer l'expression permettant de décrire l'évolution de la concentration CT du traceur à la sortie du réacteur avec ce modèle et identifier les paramètre m et n à partir des résultats expérimentaux de l'essai à blanc.

  3. Déterminer, avec ce modèle, quel devrait être le taux de conversion en sortie en régime permanent et comparer ce taux de conversion à celui obtenu pour un modèle de type réacteur parfaitement agité.

Illustration du modèle de Cholette et CloutierInformations