Génie de la Réaction Chimique : les réacteurs homogènes

Cette méthode consiste à approximer l'aire sous-tendue à une courbe par le trapèze correspondant, comme illustré ci-dessous.

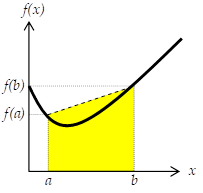
Ainsi, \(\int\limits_{a}^{b}{f(x)\cdot dx}\approx \frac{\left( f(a)+f(b) \right)\cdot \left( b-a \right)}{2}\left( =\frac{\left( grande\ base+petite\ base \right)\cdot hauteur}{2} \right)\)

On aura bien sûr une meilleure précision si on "découpe" l'intervalle [a,b] en petits intervalles :

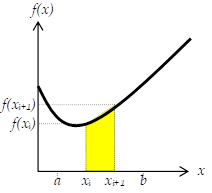
\(\int\limits_{a}^{b}{f(x)\cdot dx}\approx \sum\limits_{i}{\frac{\left( f({{x}_{i}})+f({{x}_{i+1}}) \right)\cdot \left( {{x}_{i+1}}-{{x}_{i}} \right)}{2}}\)

Généralement on prend une valeur de constante, que l'on appelle le pas.

Il existe des méthodes plus sophistiquées pour approximer l'aire sous la courbe :

\(\int\limits_{a}^{b}{f(x)\cdot dx}\approx \sum\limits_{i=0}^{n-1}{\left( \frac{h}{s}\cdot \sum\limits_{j=0}^{m}{\left( {{\sigma }_{j}}\cdot f\left( {{x}_{i}}+j\cdot h \right) \right)} \right)}\) avec \(h=\frac{\delta }{m}\)

Le pas d'intégration vaut \(\delta =\frac{b-a}{n}\), où n est le nombre de pas d'intégration dans l'intervalle [\(a\),\(b\)].

Chaque valeur \(x_i\) peut être calculée comme suit : \(x_i = a + i \cdot \delta\).

Les valeurs de \(m\), \(s\) et des \(\sigma_j\) sont données dans le tableau suivant, pour chaque méthode :