Génie de la Réaction Chimique : les réacteurs homogènes

Cette méthode permet de résoudre une équation du type \(f\left( x \right)=0\) dans un intervalle [a,b]. Il faut qu'il existe une solution unique dans cet intervalle, la première condition est donc que \(f\left( a \right)\cdot f\left( b \right)<0\).

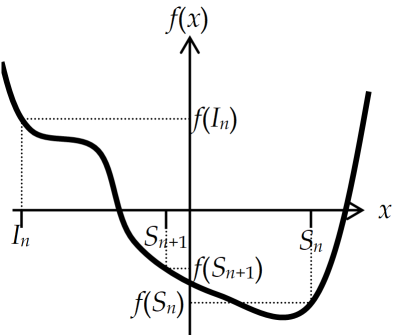
La méthode est la suivante : on cherche à réduire l'intervalle [I_n,S_n] (initialement [a,b]) dans lequel se trouve la solution jusqu'à ce que \({{S}_{n}}-{{I}_{n}}\) soit inférieur à la précision \(\varepsilon\) que l'on souhaite pour la solution. On teste si \(f\left( {{I}_{n}} \right)\cdot f\left( \frac{{{I}_{n}}+{{S}_{n}}}{2} \right)<0\) (c'est le cas de la figure précédente), dans ce cas la solution se trouve dans l'intervalle \(\left[ {{I}_{n}},\frac{{{I}_{n}}+{{S}_{n}}}{2} \right]\), par conséquent \({{I}_{n+1}}={{I}_{n}}\) et \({{S}_{n+1}}=\frac{{{I}_{n}}+{{S}_{n}}}{2}\) ; sinon \({{I}_{n+1}}=\frac{{{I}_{n}}+{{S}_{n}}}{2}\) et \({{S}_{n+1}}={{S}_{n}}\). On recommence tant que \({{S}_{n}}-{{I}_{n}}>\varepsilon\).

Cette méthode permet de résoudre une équation du type \(f\left( x \right)=0\), à condition que l'on puisse calculer la dérivée f' de la fonction f.

La méthode est la suivante : on part d'une valeur initiale x₀. La formule d'itération est : \({{x}_{k+1}}={{x}_{k}}-\frac{f\left( {{x}_{k}} \right)}{f'\left( {{x}_{k}} \right)}\). On recommence tant que la différence \(\left| {{x}_{k}}-{{x}_{k-1}} \right|\) est supérieure à la précision souhaitée.