Recherche d'optimum
Méthode dichotomique
Cette méthode permet de déterminer l'optimum d'une fonction à condition que cet optimum soit unique dans l'intervalle de recherche [a,b].
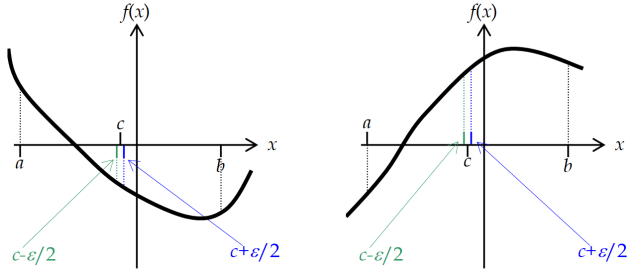
La méthode est la suivante : on sépare l'intervalle initial [a,b] en deux en plaçant \(c=\frac{b-a}{2}\) puis on calcule \(c-\frac{\varepsilon }{2}\) et \(c+\frac{\varepsilon }{2}\) (\(\varepsilon\) étant la précision souhaitée pour la détermination de l'optimum).
Si on cherche un minimum et si \(f\left( c-\frac{\varepsilon }{2} \right)>f\left( c+\frac{\varepsilon }{2} \right)\) (c'est le cas de la figure de gauche), c'est que l'optimum se trouve dans l'intervalle [c,b] qui devient le nouvel intervalle de recherche ; sinon le nouvel intervalle de recherche est [a,c].
Si on cherche un maximum et si \(f\left( c-\frac{\varepsilon }{2} \right)<f\left( c+\frac{\varepsilon }{2} \right)\) (c'est le cas de la figure de droite), c'est que l'optimum se trouve dans l'intervalle [c,b] qui devient le nouvel intervalle de recherche ; sinon le nouvel intervalle de recherche est [a,c].
On calcule le milieu du nouvel intervalle, et ainsi de suite.
On recommence tant que la longueur de l'intervalle est supérieure à \(\varepsilon\).
Méthode du nombre d'or
Cette méthode permet également de déterminer l'unique optimum d'une fonction dans l'intervalle [a,b].
Cette fois on sépare l'intervalle de recherche en trois selon le nombre d'or \(\frac{\sqrt{5}-1}{2}\approx 0,618\) : \({{x}_{1}}=b-\frac{\sqrt{5}-1}{2}\cdot \left| b-a \right|\) et \({{x}_{2}}=a+\frac{\sqrt{5}-1}{2}\cdot \left| b-a \right|\).
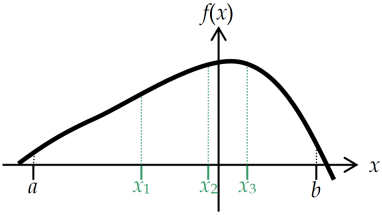
Si on cherche un maximum et si \(f\left( {{x}_{1}} \right)<f\left( {{x}_{2}} \right)\), c'est que l'optimum se trouve dans l'intervalle [x1,b] qui devient le nouvel intervalle de recherche ; sinon le nouvel intervalle de recherche est [a,x2].
On sépare le nouvel intervalle selon le nombre d'or, la particularité étant qu'une valeur est déjà connue (x2 pour le cas de la figure), ce qui limite le calcul de la fonction à 1 point supplémentaire au lieu de 2 avec la méthode dichotomique.
On recommence tant que la longueur de l'intervalle est supérieure à \(\varepsilon\).