La loi cinétique est d'ordre zéro : \(r = k\)
\(\Delta \nu =\) 1, donc à \(P\) et \(T\) constantes, \(V = V_0 \cdot (1+X_A)\)
Le bilan en réactif A s'écrit donc :
\(-k \cdot V_0 \cdot \left( 1+X_A \right) = \frac{\mathrm{d} \left[ n_{A0} \cdot \left( 1-X_A \right) \right]}{\mathrm{d} t} = -n_{A0} \cdot \frac{\mathrm{d} X_A}{\mathrm{d} t}\)
Soit, \(\frac{k \cdot V_0}{n_{A0}} \cdot \mathrm{d} t = \frac{\mathrm{d} X_A}{1+X_A} = \frac{\mathrm{d} \left( 1+X_A \right)}{1+X_A}\)
Après intégration, \(\frac{k \cdot V_0}{n_{A0}} \cdot \left( t - 0 \right) =\ln \ \left( \frac{1+X_A}{1} \right)\)
D'où \(X_A =\exp \ \left( \frac{k \cdot V_0}{n_{A0}} \cdot t \right) - 1\).
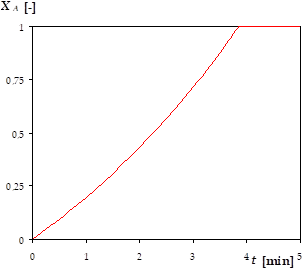
On remarque que ce taux de conversion vaut 1 pour un temps fini \(t_1\), tel que \(\exp \ \left( \frac{k \cdot V_0}{n_{A0} \cdot t_1} \right) = 2\), soit \(t_1 = \frac{\ln \ 2 \cdot n_{A0}}{k \cdot V_0}\)
Si par exemple \(k =\) 0,1 mol m-3 s-1, \(n_{A0} =\) 10 mol, \(V_0 =\) 300 L, ce temps au bout duquel la conversion est complète vaut \(t_1 =\) 231 s.
