Pertes de charge dues aux variations de direction de conduite
On liste ici quelques corrélations issues de la littérature.
Coudes
Notion fondamentale :
Le passage dans un coude peut générer beaucoup de pertes de charge.
Voici deux exemples illustrés par des animations :
coude brusque
coude arrondi
Observez les animations pour comprendre comment le changement de direction génère des turbulences et donc des pertes de charge.
Impossible d'accéder à la ressource audio ou vidéo à l'adresse : http://gpip.cnam.fr/ressources-pedagogiques-ouvertes/hydraulique/animations/coudeBrusque/ANIMATIONcoudeBrusque.mp4
La ressource n'est plus disponible ou vous n'êtes pas autorisé à y accéder. Veuillez vérifier votre accès puis recharger le média.
Impossible d'accéder à la ressource audio ou vidéo à l'adresse : http://gpip.cnam.fr/ressources-pedagogiques-ouvertes/hydraulique/animations/coudeArrondi/ANIMATIONcoudeArrondi.mp4
La ressource n'est plus disponible ou vous n'êtes pas autorisé à y accéder. Veuillez vérifier votre accès puis recharger le média.
Corrélations
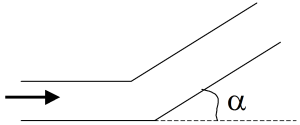
Dans le cas d'un coude brusque (c'est-à-dire à angles vifs, comme le montre la figure ci-contre), le coefficient de singularité peut alors être estimé selon : \(k=1,3\cdot \left( 1-\cos \ \alpha \right)\).
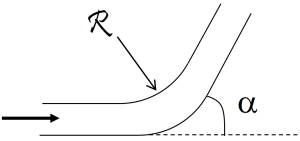
Si le coude est arrondi, on a :
\(k=\left\{ \begin{array}{r l}& \left[ 0,13+1,85\cdot {{\left( \frac{D}{2\cdot \mathcal{R}} \right)}^{3,5}} \right]\cdot \frac{\alpha}{90}\quad - \quad \rm{en\ \ r\acute{e}gime\ \ hydrauliquement\ \ lisse} \\& 0,42\cdot {{\left( \frac{D}{\mathcal{R}} \right)}^{0,5}}\quad - \quad \rm{en\ \ r\acute{e}gime\ \ hydrauliquement\ \ rugueux} \\\end{array} \right.\)
où \(\mathcal{R}\)[4] est le rayon de courbure du coude et \(\alpha\) l'angle du coude (en °).
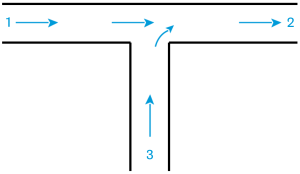
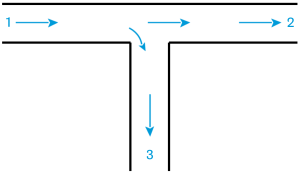
Jonctions de conduites
Méthode :
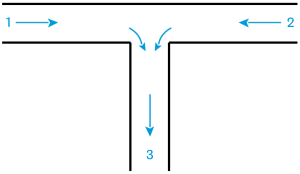
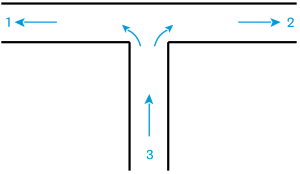
Les relations utiles pour le calcul des coefficients de singularité pour les jonctions de conduites sont données sur la figure ci-dessous.
Pour une jonction à confluent symétrique, les coefficients de singularité sont :
\(k_{13} = 2 + 3 \cdot \left[ \left( \frac{Q_{v1}}{Q_{v3}} \right)^2 - \frac{Q_{v1}}{Q_{v3}} \right]\)
\(k_{23} = 2 + 3 \cdot \left[ \left( \frac{Q_{v2}}{Q_{v3}} \right)^2 - \frac{Q_{v2}}{Q_{v3}} \right]\)
avec la perte de charge à calculer selon : \(\Delta{P_{fi3}} = k_{i3} \cdot \frac{\rho \cdot u_3^2}{2}\)
Pour une jonction à séparation symétrique, les coefficients de singularité sont :
\(k_{31} = 1 + 0,3 \cdot \left( \frac{Q_{v1}}{Q_{v3}} \right)^2\)
\(k_{32} = 1 + 0,3 \cdot \left( \frac{Q_{v2}}{Q_{v3}} \right)^2\)
avec la perte de charge à calculer selon : \(\Delta{P_{f3i}} = k_{3i} \cdot \frac{\rho \cdot u_3^2}{2}\)
Pour une jonction à confluent latéral, les coefficients de singularité sont :
\(k_{12} = 2 \cdot \frac{Q_{v3}}{Q_{v2}} - \left( \frac{Q_{v3}}{Q_{v2}} \right)^2\)
\(k_{32} = 0,6 \cdot \left[-1 + 5 \cdot \frac{Q_{v3}}{Q_{v2}} - 2 \cdot \left( \frac{Q_{v3}}{Q_{v2}} \right)^2 \right]\)
avec la perte de charge à calculer selon : \(\Delta{P_{fi2}} = k_{i2} \cdot \frac{\rho \cdot u_2^2}{2}\)
Pour une jonction à séparation latérale, les coefficients de singularité sont :
\(k_{13} = 1 + \left( \frac{Q_{v3}}{Q_{v1}} \right)^2\)
\(k_{12} = 0,4 \cdot \left( \frac{Q_{v3}}{Q_{v1}} \right)^2\)
avec la perte de charge à calculer selon : \(\Delta{P_{f1i}} = k_{1i} \cdot \frac{\rho \cdot u_1^2}{2}\)
