Associations de conduites
Notion fondamentale : Additivité des pertes de charge
Pour calculer la perte de charge totale d'un circuit, on utilise l'additivité des pertes de charge :
\(\Delta {{P}_{f}}=\Delta {{P}_{fr}}+\sum{\Delta {{P}_{fs}}}=\frac{\rho \cdot {{\overline{u}}^{2}}}{2}\cdot \left( \frac{8\cdot {}^{f}/{}_{2}\cdot L}{D}+\sum{k} \right)\)
Il faut toutefois souligner que l'additivité des pertes de charge singulières n'est strictement vraie que si les singularités sont suffisamment éloignées les unes des autres pour que la perturbation de l'écoulement due à une singularité soit estompée avant que le fluide n'arrive à la singularité suivante. On préconise généralement une distance de 5 à 10 fois le diamètre de la conduite entre les singularités pour que ceci soit vrai.
Cependant en pratique, comme il n'est pas possible (sauf par le biais de calculs de mécanique des fluides numériques assez poussés) de faire un autre calcul des pertes de charge lorsque les singularités sont proches les unes des autres, on utilise malgré tout l'additivité précédente, tout en sachant qu'il s'agit d'une approximation.
Association de conduites en série
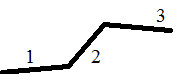
Pour une association de conduites en série, on a :
\(\left\{ \begin{array}{r l}& {{Q}_{v}}={{Q}_{v1}}={{Q}_{v2}}={{Q}_{v3}} \\& \Delta P=\Delta {{P}_{1}}+\Delta {{P}_{2}}+\Delta {{P}_{3}} \\\end{array} \right.\)
\({Q}_{v1}\), \({Q}_{v2}\) et \({Q}_{v3}\) étant les débits dans chaque portion du circuit et \(\Delta {{P}_{1}}\), \(\Delta {{P}_{2}}\) et \(\Delta {{P}_{3}}\) les variations de pression sur chaque tronçon,
\({Q}_{v}\) et \(\Delta {P}\) respectivement le débit total et la variation de pression sur le circuit.
Association de conduites en parallèle
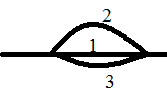
Pour une association de conduites en parallèle, on a :
\(\left\{ \begin{array}{r l}& {{Q}_{v}}={{Q}_{v1}}+{{Q}_{v2}}+{{Q}_{v3}} \\& \Delta P=\Delta {{P}_{1}}=\Delta {{P}_{2}}=\Delta {{P}_{3}} \\\end{array} \right.\)