Courbes caractéristiques d'une pompe centrifuge
Pour caractériser une pompe centrifuge, on s'appuie sur trois courbes caractéristiques.
Impossible d'accéder à la ressource audio ou vidéo à l'adresse :
La ressource n'est plus disponible ou vous n'êtes pas autorisé à y accéder. Veuillez vérifier votre accès puis recharger le média.
Caractéristique
Selon l'équation de Bernouilli généralisée (utilisée ici un peu abusivement car l'écoulement dans une pompe centrifuge n'a rien d'irrotationnel, mais ceci permet de comprendre le principe), si les conduites d'aspiration et de refoulement d'une pompe ont le même diamètre, on peut écrire :
\({{P}_{ref}}-{{P}_{asp}}=\rho \cdot g\cdot {{H}_{mt}^{theorique}}-\Delta P_{f}^{pompe}=\rho \cdot g\cdot {{H}_{mt}}\)
On en déduit que la hauteur manométrique totale (vraie) décroît avec le débit, du fait des pertes par frottement dans la pompe. La courbe donnant cette hauteur manométrique totale en fonction du débit est appelée caractéristique de la pompe et a l'allure représentée sur la figure ci-dessous.

Rendement
Définition :
Le rendement \(\eta\)[3] d'une pompe est défini comme le rapport de la puissance fournie au fluide \(\mathcal{P}_{hydro}\) et de la puissance absorbée par la pompe \(\mathcal{P}_{abs}\) : \(\eta=\frac{\mathcal{P}_{hydro}}{\mathcal{P}_{abs}}\)
La puissance fournie au fluide étant la suivante : \(\mathcal{P}_{hydro}=Q_{v} \cdot \rho \cdot g\cdot {{H}_{mt}} = Q_{v} \cdot \Delta{P_{pompe}}\).
Puisque la hauteur manométrique totale \({H}_{mt}\) décroît avec le débit \(Q_{v}\), la courbe \(\eta\) vs \(Q_{v}\) présente un maximum, comme illustré sur la figure ci-dessous.

NPSH
Définition : NPSH
Si l'on appelle \(\Delta\) la dépression locale maximale qui peut avoir lieu dans la pompe, pour éviter le phénomène de cavitation, il faut que la pression d'aspiration \(P_{asp}\) soit telle que \(P_{asp} – \Delta > P_{vap}\) (où \(P_{vap}\)[5] est la pression de vapeur saturante, à la température considérée). On définit le \(NPSH\)[6] (net positive suction head) selon :
\(NPSH=\frac{P_{asp}}{\rho \cdot g} - \frac{P_{vap}}{\rho \cdot g}\)
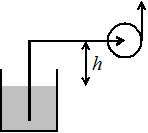
Considérons le circuit représenté ci-contre, pour lequel on suppose que la surface du réservoir est à la pression atmosphérique et que le niveau dans le réservoir est à peu près constant (donc vitesse nulle à la surface libre). L'équation de Bernouilli pour un fluide réel fournit :
\(\frac{P_{atm}}{\rho \cdot g}+\frac{{{0}^{2}}}{2\cdot g}=\frac{P_{asp}}{\rho \cdot g}+h +\frac{{{u_{asp}}^{2}}}{2\cdot g}+ \frac{\Delta{P_{f}^{asp}}}{\rho \cdot g}\)
\(\Delta{P_{f}^{asp}}\) étant ici la perte de charge totale sur le circuit d'aspiration.
Ainsi \(\frac{P_{asp}}{\rho \cdot g}=\frac{P_{atm}}{\rho \cdot g} -h -\frac{{{u_{asp}}^{2}}}{2\cdot g} - \frac{\Delta{P_{f}^{asp}}}{\rho \cdot g}\)
La condition précédente \(P_{asp} – \Delta > P_{vap}\) devient alors :
\(\frac{P_{atm}}{\rho \cdot g} -h -\frac{{{u_{asp}}^{2}}}{2\cdot g} - \frac{\Delta{P_{f}^{asp}}}{\rho \cdot g} – \frac{\Delta}{\rho \cdot g} > \frac{P_{vap}}{\rho \cdot g}\)
Ou encore : \(\frac{P_{atm}}{\rho \cdot g} -h - \frac{{{u_{asp}}^{2}}}{2\cdot g} - \frac{\Delta{P_{f}^{asp}}}{\rho \cdot g} - \frac{P_{vap}}{\rho \cdot g} > \frac{\Delta}{\rho \cdot g}\)
Définition :
On nomme \(NPSH_{disponible}\) le terme de gauche et \(NPSH_{requis}\) celui de droite.
En pratique le \(NPSH_{requis}\) est donné par le fournisseur de la pompe parce qu'il la caractérise.
Alors que le \(NPSH_{disponible} = \frac{P_{asp}}{\rho \cdot g} - \frac{P_{vap}}{\rho \cdot g}\) caractérise le circuit sur lequel est installé la pompe (le circuit d'aspiration en l’occurrence) et doit donc être calculé par l'utilisateur.
Remarque :
On peut rencontrer une définition du NPSH disponible, où on considère que l'énergie cinétique disponible à l'aspiration peut être convertie en énergie de pression pour éviter la vaporisation.
\(NPSH_{dispo}=\frac{P_{asp}}{\rho \cdot g} + \frac{{{u_{asp}}^{2}}}{2\cdot g} - \frac{P_{vap}}{\rho \cdot g}\)
Conseil :
Pour éviter la cavitation, il faut par conséquent de préférence :
monter la pompe en charge (pour que la hauteur \(h\) soit négative et de valeur absolue maximale) ;
travailler à basse température (où la pression de vapeur saturante \(P_{vap}\) est plus faible) ;
limiter les pertes de charge \(\Delta{P_{f}^{asp}}\) sur le circuit d'aspiration (et notamment éviter d'y placer une vanne).
Notion fondamentale :
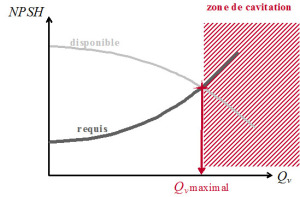
Le \(NPSH_{disponible}\) dépend du circuit d'aspiration et du débit, tandis que le \(NPSH_{requis}\) dépend de la pompe et du débit. Pour un circuit d'aspiration et une pompe donnés, il existe un débit maximum admissible, comme le montre la figure ci-contre.
Courbes caractéristiques d'une pompe centrifuge
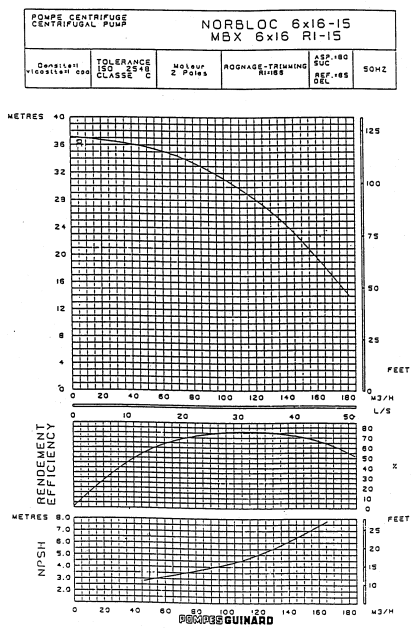
Le fabriquant d'une pompe doit donc fournir des séries de courbes telles que celles présentées sur la figure ci-dessous. En effet, une caractéristique, une courbe \(\eta\) vs \(Q_{v}\), ou une courbe \(NPSH_{requis}\) vs \(Q_{v}\), sont valables pour une pompe donnée, fonctionnant à une vitesse de rotation donnée, mais aussi pour un fluide donné (masse volumique et viscosité).