Calcul des pertes de charge régulières en régime turbulent
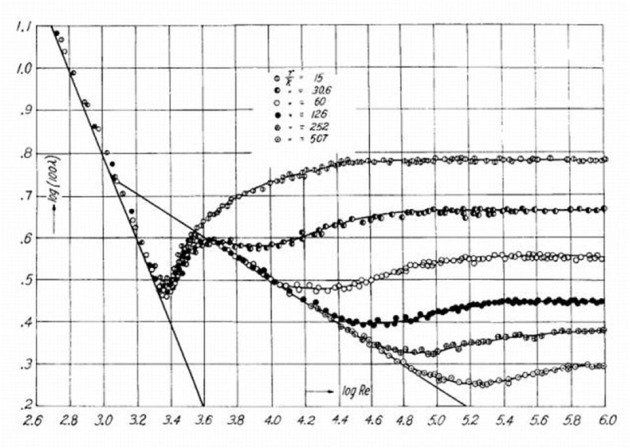
Contrairement au régime laminaire, en régime turbulent les pertes de charge régulières peuvent dépendre de l'état de surface de la conduite. Nikuradse a mesuré les pertes de charge régulières en fonction du nombre de Reynolds en rendant artificiellement des conduites rugueuses en collant sur la surface interne des grains de sable de taille calibrée. Il distingue deux régimes, l'un est dit hydrauliquement lisse (le facteur de frottement est indépendant de la rugosité), et l'autre est dit hydrauliquement rugueux (\(f/2\) dépend de la rugosité de la conduite).
Rugosité
Définition :
Exemple :
On peut donner quelques ordres de grandeur de rugosité des matériaux couramment utilisés pour les conduites dans les procédés :
tube étiré (verre, cuivre, laiton) : \(e\) < 0,001 mm ;
tube acier : neuf : \(e\) = 0,05 mm ; rouillé : \(e\) = 0,15 à 0,25 mm ; encrassé : \(e\) = 1,5 à 3 mm ;
tube fonte neuf : \(e\) = 0,25 mm ; rouillé : \(e\) = 1 à 1,5 mm ;
tube ciment : \(e\) = 0,3 à 3 mm ;
pierre de taille : \(e\) = 3 à 15 mm.
Diagramme de Moody
Nikuradse a réalisé des expériences dans des tubes de rugosité variable. Les résultats sont montrés sur le diagramme suivant.
Notion fondamentale :
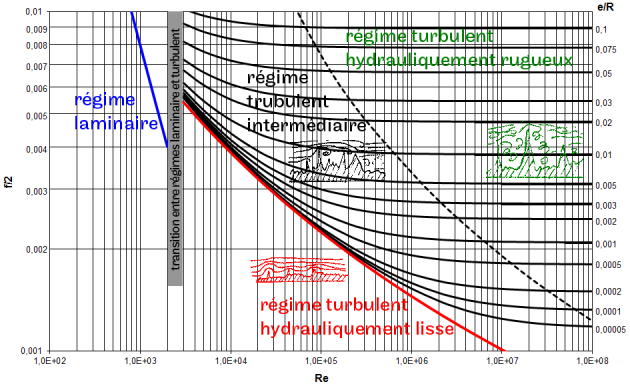
Le diagramme de Moody regroupe des relations rapportées dans la littérature pour calculer le facteur de frottement selon les valeurs de nombre de Reynolds \(Re\) et la rugosité réduite \(\frac{e}{R}\).
Attention : Courbes iso-rugosités relatives
\(e/R\) n'est pas sur l'axe vertical, les valeurs se rapportent aux courbes, qui sont donc des "iso-rugosités relatives".
Notion fondamentale :
Le diagramme de Moody met en évidence trois sous-régimes d'écoulement en régime turbulent :
régime hydrauliquement lisse 
régime intermédiaire 
régime hydrauliquement rugueux 
Le régime hydrauliquement lisse comporte deux zones, la première étant représentée par la droite de Blasius.
Si la rugosité croît, le facteur de frottement également, donc les pertes de charge augmentent. On note que, en régime intermédiaire, si le nombre de Reynolds croît, le facteur de frottement décroît ; par conséquent, en augmentant (par exemple) la vitesse d'écoulement, le facteur de frottement décroît. MAIS ATTENTION, cela ne signifie pas que les pertes de charge diminuent, bien au contraire !
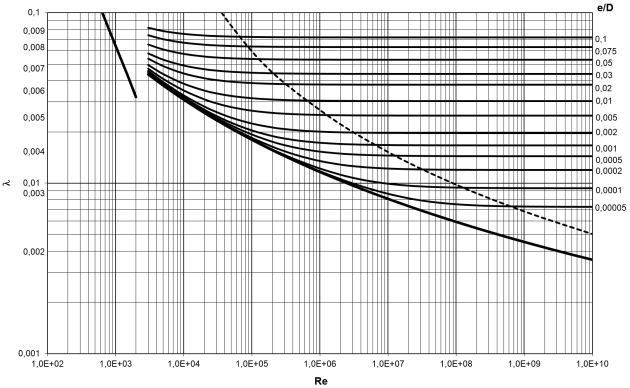
Remarque : Diagramme de Moody en coefficient de perte de charge
Le diagramme de Moody suivant montre le coefficient de frottement \(\lambda\) selon les valeurs de nombre de Reynolds \(Re\) et la rugosité relative \(\frac{e}{D}\).
Expressions permettant le calcul du facteur de frottement
Notion fondamentale :
On calcule le facteur de frottement à partir de nombre de Reynolds \(\rm{Re}\) et la rugosité réduite \(\frac{e}{R}\) (ou \(\frac{e}{D}\)), selon le régime d'écoulement :
régime hydrauliquement lisse :
\(\frac{1}{\sqrt{{f}/{2}}}=2,46\cdot \ln \ \left( Re\cdot \sqrt{{f}/{2}} \right)+0,29\) 1e relation de Nikuradzé (c'est une expression implicite[5])
droite de Blasius, utilisable dans la zone linéaire, soit pour des nombres de Reynolds compris entre 3000 et 105 :
\(f/2=0,0395\cdot Re^{-0,25}\) ou encore \(\lambda=\frac{0,316}{Re^{-0,25}}\)
relation de Karman-Nikuradzé, utilisable pour des nombres de Reynolds compris entre 105 et 108 :
\(\lambda=0,0032+\frac{0,221}{Re^{0,237}}\) soit \(f/2=0,0004+\frac{0,0276}{Re^{0,237}}\)
régime intermédiaire :
\(\frac{1}{\sqrt{f/2}}=2,457\cdot \ln \ {{\left[ {{\left( \frac{7}{Re} \right)}^{0,9}}+0,27\cdot \frac{e}{D} \right]}^{-1}}\) relation de Churchill
régime hydrauliquement rugueux :
\(\frac{1}{\sqrt{f/2}}=2,46\cdot \ln \ \left( \frac{R}{e} \right)+4,92\) 2e relation de Nikuradse
Relation de Colbrook
Méthode :
En général, on utilise le diagramme de Moody pour déterminer le régime d'écoulement et l'ordre de grandeur du facteur de frottement ; puis on utilise la corrélation appropriée ci-dessus pour faire un calcul plus précis.
Remarque :
À l'aide du diagramme de Moody, on peut :
calculer la perte de charge dans des conditions opératoires données ;
évaluer la rugosité d'une conduite (à partir d'une mesure de perte de pression en régime hydrauliquement rugueux) ;
calculer le débit susceptible de s'écouler dans une conduite pour une perte de charge et une rugosité données ;
etc.
Ces différentes possibilités feront l'objet d'exercices dans la suite de ce module.
Cas des conduites non-circulaires
Remarque :
Comme nous l'avons déjà mentionné précédemment, dans le cas de conduites non-circulaires, on calcule le diamètre hydraulique[6] \(D_{h}\). Puis on applique les mêmes relations que précédemment.
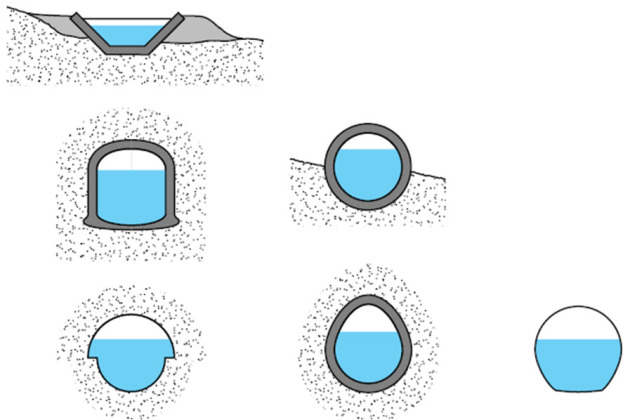
Cas des canaux ouverts
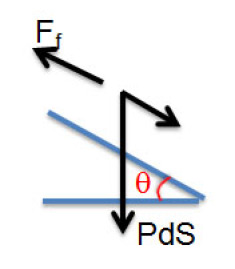
Dans le cas d'un canal ouvert de faible pente (\(l = sin \theta\)), le bilan des forces en régime stationnaire fera apparaître :
le poids : \(m \cdot g \cdot sin \theta\)
la force de frottement = contrainte × surface frottement, où la surface frottement dépend du périmètre mouillé et où la contrainte est fournie par \(f/2 \cdot \rho \cdot u^{2}\)
Le facteur de frottement en régime laminaire valant \(f/2 = \frac{8}{Re}\), la relation de Chézy fournit la vitesse du fluide :
\(C \cdot \sqrt{R_{H} \cdot sin \theta}\)
Ainsi le débit volumique dans le canal est : \(Q_{v} = C \cdot S \cdot \sqrt{R_{H} \cdot l}\)
Le coefficient de Chézy est donné par la formule de Bazin : \(C = \frac {87} {1 + \frac{\gamma}{\sqrt{R_{H}}}}\)
