Pertes de charge dans des conduites diverses
On s'intéresse à des écoulements d'eau à la vitesse moyenne de 1 m/s dans des conduites circulaires.
Question
Calculer la perte de charge engendrée par mètre linéaire dans une conduite en fonte de 20 cm de diamètre.
Résultat
55 Pa m-1
Solution
\(Re=\)2 105 et \(\frac{e}{R}=\)0,0025, on lit alors sur le diagramme de Moody \({}^{f}/{}_{2}\approx \)0,0027
Compte tenu de la position du point, le régime est intermédiaire, on utilise donc la relation de Churchill pour effectuer un calcul plus précis : \({}^{f}/{}_{2}=\)2,765 10-3
Finalement on évalue la perte de charge : \(\Delta {{P}_{fr}}=\) 55 Pa m-1
Solution détaillée
\(Re=\frac{\rho \cdot \overline{u}\cdot D}{\mu }=\frac{1000\times 1\times 20\ {{10}^{-2}}}{{{10}^{-3}}}=\)2 105 et \(\frac{e}{R}=\frac{0,25\ {{10}^{-3}}}{{}^{20\ {{10}^{-2}}}/{}_{2}}=\)0,0025
On place le point correspondant sur le diagramme de Moody (en rouge), et on lit l'ordre de grandeur du facteur de frottement \({}^{f}/{}_{2}\approx\)0,0027. On constate que le point est situé dans la zone correspondant que régime intermédiaire.
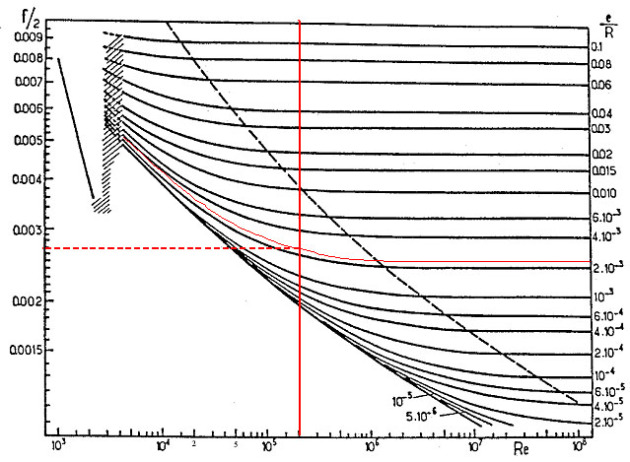
La relation de Churchill fournit une valeur plus précise :
\({}^{f}/{}_{2}={{\left( 2,457\cdot \ln \ {{\left[ {{\left( \frac{7}{Re} \right)}^{0,9}}+0,27\cdot \frac{e}{D} \right]}^{-1}} \right)}^{-2}}={{\left( 2,457\cdot \ln \ {{\left[ {{\left( \frac{7}{2\ {{10}^{5}}} \right)}^{0,9}}+0,27\cdot \frac{0,25\ {{10}^{-3}}}{20\ {{10}^{-2}}} \right]}^{-1}} \right)}^{-2}}=\)2,765 10-3
On en déduit la perte de charge engendrée par mètre linéaire de conduite :
\(\Delta {{P}_{fr}}={}^{f}/{}_{2}\cdot \left( 4\cdot \rho \cdot {{\overline{u}}^{2}} \right)\cdot \frac{L}{D}=2,765\ {{10}^{-3}}\times \left( 4\times 1000\times {{1}^{2}} \right)\times \frac{1}{20\ {{10}^{-2}}}=\)55 Pa m-1
Question
Même question pour une conduite en acier neuve de 1 cm de diamètre.
Résultat
1917 Pa m-1
Solution
\(Re=\)104 et \(\frac{e}{R}=\)0,01 ; on lit sur le diagramme de Moody \({}^{f}/{}_{2}\approx \)0,0047
régime intermédiaire (relation de Churchill) \({}^{f}/{}_{2}=\)4,793 10-3
\(\Delta {{P}_{fr}}=\)1917 Pa m-1
Solution détaillée
On procède de même : \(Re=\frac{1000\times 1\times 1\ {{10}^{-2}}}{{{10}^{-3}}}=\)104 ; \(\frac{e}{R}=\frac{0,05\ {{10}^{-3}}}{{}^{1\ {{10}^{-2}}}/{}_{2}}=\)0,01
En vert sur le diagramme de Moody, \({}^{f}/{}_{2}\approx \)0,0047. Le régime est également intermédiaire.
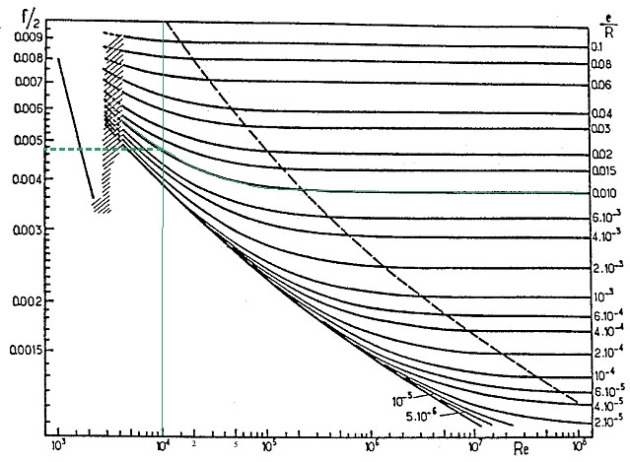
\({}^{f}/{}_{2}={{\left( 2,457\cdot \ln \ {{\left[ {{\left( \frac{7}{{{10}^{4}}} \right)}^{0,9}}+0,27\cdot \frac{0,05\ {{10}^{-3}}}{1\ {{10}^{-2}}} \right]}^{-1}} \right)}^{-2}}=\)4,793 10-3
\(\Delta {{P}_{fr}}=4,793\ {{10}^{-3}}\times \left( 4\times 1000\times {{1}^{2}} \right)\times \frac{1}{1\ {{10}^{-2}}}=\)1917 Pa m-1