Notions de dimensions
Notion fondamentale : Systèmes d'unités
Pour toute grandeur physique, les unités interviennent : elles sont essentielles à la quantification de cette grandeur.
Un système d'unités est un ensemble d'unités cohérentes entre elles afin de définir l'ensemble des grandeurs observées. On compte plusieurs systèmes d'unités, principalement le système métrique et le système impérial (encore très présent dans les pays anglo-saxons) mais pas seulement : dans le système métrique, les physiciens utilisent le système MKS (pour Mètre - Kilogramme - Seconde) et les chimistes le système CGS (pour Centimètre - Gramme - Seconde).
Même si cela peut paraître simple, les conversions entre unités ou les transformations de relations empiriques demande une certaine rigueur pour leur traitement. Dans ces cas là, les handbooks proposent des tables de conversion conséquentes qui peuvent s’avérer utiles.
Définition : Dimension
On appelle dimension, le rapport entre l'unité de la grandeur et les sept unités de base du système internationnal, à savoir :
Dimension | Symbole de la dimension | Unité S.I. |
Masse | M | kilogramme |
Temps | T | seconde |
Longueur | L | mètre |
Température | θ | Kelvin |
Intensité électrique | I | Ampère |
Quantité de matière | n | mole |
Intensité lumineuse | J | Candela |
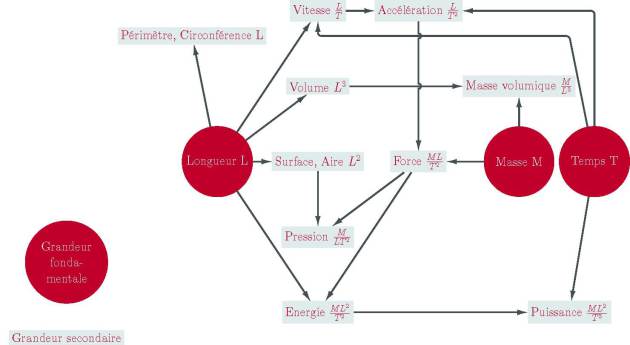
Pour les sept dimensions de ce tableau on parle de grandeurs fondamentales, pour toutes les autres on parlera de grandeurs secondaires, car elles sont obtenues par composition des sept fondamentales.
Exemple : Exemples de dimensions secondaires
On calcule l'aire d'une surface \(S\) comme le produit de deux longueurs, donc : \([\text{S}]=L^2\)
On calcule une vitesse \(u\) comme la longueur parcourue au cours d'un temps donnée, donc :
On calcule une masse volumique \(\rho\) comme le entre une masse et un volume, donc :