Des profils de vitesse à la notion de couche limite
Le vidéo suivante introduit les notions de profils de vitesse et de couche limite.
Impossible d'accéder à la ressource audio ou vidéo à l'adresse :
La ressource n'est plus disponible ou vous n'êtes pas autorisé à y accéder. Veuillez vérifier votre accès puis recharger le média.
La viscosité engendre un gradient de vitesse dans une section droite de conduite :
à la paroi, la vitesse du fluide est nulle (c'est la
condition d'adhérence) ;la vitesse est maximale au centre de la conduite.
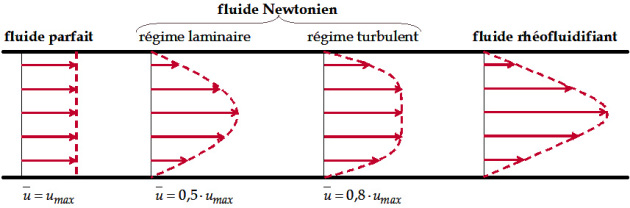
La figure ci-dessous montre les différents types de profils rencontrés en fonction du type de fluide et du régime d'écoulement.
Vitesse moyenne
Définition : Vitesse moyenne
Du fait qu'il existe un gradient de vitesse au sein des fluides qui s'écoulent dans le conduite, on définit la vitesse moyenne d'écoulement \(\overline{u}\)[3].
Cette vitesse est directement reliée au débit volumique. Ainsi dans une conduite circulaire de diamètre \(D\), la vitesse moyenne d'écoulement est telle que \(Q_{v}=\overline{u} \cdot \frac{\pi \cdot D^{2}}{4}\).
Notion de couche limite
La notion de couche limite est très importante en génie des procédés, car c'est dans cette couche que se trouvent généralement les plus importantes résistances aux transferts de matière et de chaleur. Cette partie a pour but de lister quelques corrélations utiles pour évaluer les dimensions de cette couche.
Définition : Couche limite
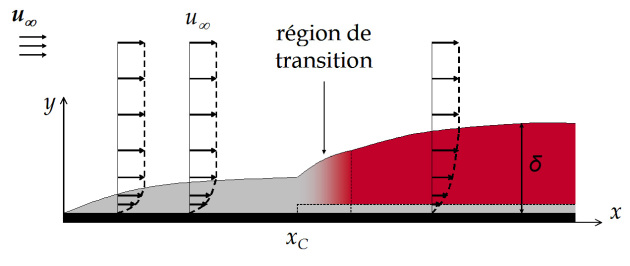
Considérons un fluide qui s'écoule le long d'une surface solide plane placée dans le sens de l'écoulement. La vitesse du fluide est nulle à la paroi, et, du fait des frottements, croît progressivement à travers le fluide quand on s'éloigne de la paroi jusqu'à atteindre la vitesse \({u}_{\infty }\) loin de la paroi. Cet effet est considéré comme confiné dans une épaisseur de fluide appelée couche limite, voisine de la paroi solide.
On appelle \(\delta\)[5] l'épaisseur de la couche limite, elle correspond à la définition . \({{u}_{\delta }}=0,99\cdot {{u}_{\infty }}\)
Dans le cas d'une plaque plane, l'écoulement dans la couche limite est laminaire (en gris sur la figure) aux faibles distances \(x\) du bord d'attaque de la plaque, puis il est turbulent (en rouge sur la figure ci-contre) pour de grandes longueurs. Entre ces deux zones, existe une région de transition, située à une distance \(x_{c}\) du bord d'attaque, telle que :
\(3\ {{10}^{5}}<R{{e}_{c}}=\frac{\rho \cdot {{u}_{\infty }}\cdot {{x}_{c}}}{\mu }<3\ {{10}^{6}}\)
Entre la paroi et la couche limite turbulente, persiste une sous-couche limite laminaire, de faible épaisseur.
Cette théorie de la couche limite est très importante pour l'étude poussée des pompes centrifuges, des coques de bateau, des fuselages...
En génie des procédés, cette couche limite joue un rôle crucial pour les transferts de matière et de chaleur.
Couche limite sur une plaque plane
Pour une plaque plane de longueur \(L\), on dispose des corrélations qui suivent.
Méthode : Couche limite laminaire
L'épaisseur de la couche limite est donnée par la relation :
\(\frac{\delta }{x}=4,64\cdot R{{e}_{x}}^{-1/2}\)
Le coefficient de frottement (qui n'est autre que le rapport de la contrainte à la paroi par le terme d'énergie cinétique \(\frac{\rho \cdot {{u}_{\infty }}^{2}}{2}\)), est le suivant (avec \(R{{e}_{x}}=\frac{\rho \cdot u\cdot x}{\mu }\) ; \(Re=\frac{\rho \cdot u\cdot L}{\mu }\)) :
localement : \({{{}^{f}/{}_{2}}_{x}}=0,353\cdot R{{e}_{x}}^{-1/2}\) ; globalement : \({}^{f}/{}_{2}=0,646\cdot R{{e}^{-1/2}}\)
Ceci permet de calculer la contrainte au niveau de la paroi.
Méthode : Couche limite modérément turbulente
Pour \(10^5 < Re < 10^7\), l'épaisseur de la couche limite est donnée par la relation :
\(\frac{\delta }{x}=0,376\cdot R{{e}_{x}}^{-0,2}\)
L'épaisseur de la sous-couche limite laminaire est la suivante :
\(\frac{\delta }{x}=72,4\cdot R{{e}_{x}}^{-0,9}\)
Les coefficients de frottement local et global sont les suivants :
\({{{}^{f}/{}_{2}}_{x}}=0,0293\cdot R{{e}_{x}}^{-0,2}\) ; \({}^{f}/{}_{2}=0,0366\cdot R{{e}^{-0,2}}\)
Méthode : Couche limite turbulente
Pour \(10^7 < Re \), l'épaisseur de la couche limite et le coefficient de frottement global sont donnés par les expressions de Schoenhen :
\(\left\{ \begin{array}{r l}& \frac{\delta }{x}=0,54\cdot \sqrt{{}^{f}/{}_{2}} \\& \frac{0,171}{\sqrt{{}^{f}/{}_{2}}}=\log \ \left( 2\cdot Re\cdot {}^{f}/{}_{2} \right) \\\end{array} \right.\)
Méthode : Couche limite fortement turbulente
Pour \(10^7 < Re < 10^9,\) on donne l'approximation suivante, sous forme explicite (Van Karman & Schliching) :
\(\left\{ \begin{array} {r l}& \frac{\delta }{x}=0,22\cdot R{{e}_{x}}^{1/6} \\& \\& {}^{f}/{}_{2}=0,456\cdot {{\left( \log \ Re \right)}^{-2,58}} \\\end{array} \right.\)
Couche limite dans une conduite
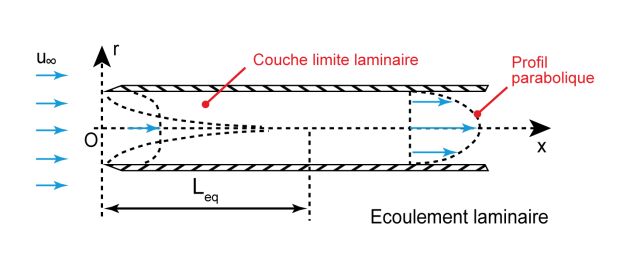
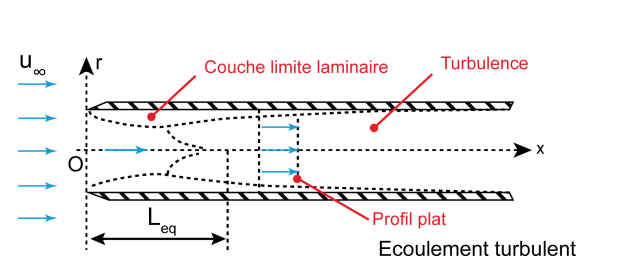
À l'intérieur d'une conduite, on observe également le développement d'une couche limite, comme le montre les figures suivantes. Toutefois, dans cette géométrie confinée, au bout d'une distance suffisamment longue par rapport à l'entrée dans la conduite, la couche limite envahit toute la conduite.
Ainsi, si la couche limite envahit toute la conduite alors que la couche limite n'était encore que laminaire, l'écoulement dans la conduite sera laminaire (figure de gauche), on comprend que ceci se produira en particulier si la conduite a un faible diamètre.
Si au contraire, la couche limite turbulente a pu se développer avant que la couche limite n'envahisse toute la conduite, l'écoulement sera turbulent (figure de droite).
L'épaisseur de la sous-couche limite laminaire dans une conduite circulaire est globalement proportionnelle à l'inverse de la vitesse moyenne, et est donnée par l'expression :
\(\frac{\delta }{D}=60\cdot R{{e}^{-7/8}}\)
Définition : Longueur d'établissement
La longueur d'établissement \({L}_{e}\) du régime d'écoulement correspond à la distance entre l'entrée dans la conduite et la position à partir de laquelle la couche limite a envahi toute la conduite. Elle est corrélée selon la valeur du nombre de Reynolds comme suit :
\(\frac{{{L}_{e}}}{D}=\left\{ \begin{array} {r l}& 0,6\quad pour\ \ Re<100 \\& \left( 0,03\ \grave{a}\ 0,06 \right)\cdot Re\quad pour\ \ 100<Re<2000 \\& \left( 0,6\ \grave{a}\ 0,8 \right)\cdot R{{e}^{1/4}}\quad pour\ \ Re>2000 \\\end{array} \right.\)