Viscosité
Expérience : Mise en évidence des frottements dans les fluides
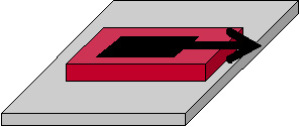
Pour mettre en évidence l'existence de frottements dans les fluides, on réalise une expérience, illustrée par la figure ci-contre : on dépose une feuille de papier aluminium (en noir sur la figure) sur une couche de miel (en rouge), le tout reposant sur un support rigide fixe (en gris).
Les grandeurs caractéristiques du problème sont :
la force appliquée pour tirer la feuille de papier aluminium ;
la vitesse u de déplacement de la feuille, qui augmente avec la force de traction ;
l'épaisseur e de la couche de miel : il faut exercer une force bien supérieure pour obtenir la même vitesse si la couche de miel est plus mince ;
la surface S de la feuille : la force nécessaire pour obtenir la même vitesse de déplacement est d'autant plus faible que la surface de la feuille est faible.
On en déduit la forme de la force exercée : F\propto S\cdot \frac{u}{e}.
L'épaisseur e étant faible, \frac{u}{e} est en fait un gradient de vitesse \frac{du}{de}.
Viscosité dynamique
Définition : Viscosité dynamique
Remarque : Unité de la viscosité dynamique
La viscosité dynamique a pour équation aux dimensions M L-1 T-1 et est généralement exprimée en Pa s (éventuellement en poise : 1 Po = 0,1 Pa s).
Exemple : Ordres de grandeur
Cette vidéo montre l'effet de la viscosité sur un cas d'étude : la chute d'une boule dans des liquides de viscosité croissante.
Les ordres de grandeur de viscosité dynamique sont les suivants dans les conditions ambiantes :
air : 2 10-5 Pa s ;
eau : 10-3 Pa s = 1 cPo (centipoise) ;
miel : 6 Pa s ;
gels : 1 à 100 Pa s ;
peintures : 10 à 1000 Pa s ;
goudrons : 100 à 105 Pa s ;
glace : 1013 Pa s ;
granit : 1020 Pa s.
Voici quelques valeurs de viscosité dynamique de liquides à 20°C :
Acétone | 0,33 10-3 Pa s |
Eau | 10-3 Pa s |
Éthanol | 1,20 10-3 Pa s |
Mercure | 1,55 10-3 Pa s |
Huile d'olive | 84 10-3 Pa s |
Glycérine | 1499 10-3 Pa s |
Voici quelques valeurs de viscosité dynamique de gaz à 20°C :
Air | 1,85 10-5 Pa s |
CO2 | 1,48 10-5 Pa s |
H2 | 0,89 10-5 Pa s |
Vapeur d'eau | 10,5 10-5 Pa s |
Remarque : Effets de la pression et la température
Pour les liquides, la viscosité dynamique diminue avec la température. En effet, lorsque la température augmente, les distances intermoléculaires augmentent (dilatation), il y a donc moins de frottements, et la viscosité diminue. En revanche la viscosité dynamique des liquides est peu sensible à la pression.
Pour les gaz, la viscosité dynamique augmente avec la pression et la température. En effet, lorsque la pression augmente, les frottements augmentent, et donc la viscosité aussi ; lorsque la température augmente, la vitesse des molécules augmente et leur taux de collision également, par conséquent la viscosité augmente.
On peut voir sur le graphique ci-dessous l'effet de la température sur la viscosité dynamique de l'eau.
Viscosité cinématique
Définition : Viscosité cinématique
Remarque : Unité de la viscosité cinématique
Elle a pour équation aux dimensions L2 T-1 et est exprimée en m2 s-1 dans le système international d'unités.
On l'exprime parfois en Stokes (St) : 1 m2 s-1 = 104 cm2 s-1 = 104 St.
Exemple : Ordre de grandeur de la viscosité cinématique
La viscosité cinématique de l'eau à 20°C est de 10-6 m2 s-1 = 1 cSt (centi-Stokes).
