Conséquences de la loi fondamentale de la statique des fluides
On se limitera désormais au cas des fluides incompressibles dans le champ de pesanteur seul.
Impossible d'accéder à la ressource audio ou vidéo à l'adresse :
La ressource n'est plus disponible ou vous n'êtes pas autorisé à y accéder. Veuillez vérifier votre accès puis recharger le média.
Principe des vases communicants
Notion fondamentale : Vases communicants à un seul fluide
Impossible d'accéder à la ressource audio ou vidéo à l'adresse :
La ressource n'est plus disponible ou vous n'êtes pas autorisé à y accéder. Veuillez vérifier votre accès puis recharger le média.
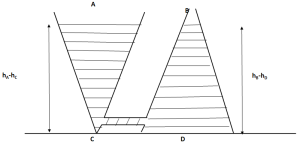
La pression au fond de 2 récipients de formes quelconques remplis sur la même hauteur et reliés par le bas à l'aide d'un tube est la même : \(P_{C} = P_{D}\).
En effet, les deux récipients étant remplis sur la même hauteur, on a : \(h_{A} - h_{C} = h_{B} - h_{D} = \Delta h\)
Dans le récipient de gauche : \(P_{C} = P_{atm} + \rho \cdot g \cdot \Delta h\).
Dans le récipient de droite : \(P_{D} = P_{atm} + \rho \cdot g \cdot \Delta h\).
Par conséquent \(P_{C} = P_{D}\).
Réciproqement, si le liquide est versé par exemple dans le récipient de droite, le niveau s'équilibrera entre les 2 récipients de sorte que la hauteur de liquide soit la même des deux côtés : \(h_{A} = h_{B}\).
Exemple : Cas de deux liquides superposés
Les fluides 1 et 2 (parfaitement immiscibles) sont placés dans un tube en U selon le schéma de droite.
\({{P}_{O}}={{P}_{A}}+{{\rho }_{1}}\cdot g\cdot h={{P}_{B}}+{{\rho }_{1}}\cdot g\cdot h\) donc \({{P}_{A}}={{P}_{B}}\)
or \({{P}_{A}}={{P}_{atm}}+{{\rho }_{2}}\cdot g\cdot {{H}_{2}}\) et \({{P}_{B}}={{P}_{atm}}+{{\rho }_{1}}\cdot g\cdot {{H}_{1}}\)
d'où \({{\rho }_{1}}\cdot {{H}_{1}}={{\rho }_{2}}\cdot {{H}_{2}}\).
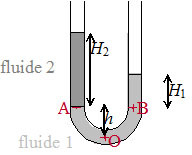
Ce dispositif peut être utilisé pour mesurer la masse volumique de l'un des deux fluides, si l'on connaît celle de l'autre fluide.
Exemple : Baromètre à mercure
Impossible d'accéder à la ressource audio ou vidéo à l'adresse :
La ressource n'est plus disponible ou vous n'êtes pas autorisé à y accéder. Veuillez vérifier votre accès puis recharger le média.
Dans un baromètre à mercure, la différence de niveau \(H\) entre les deux branches donne la pression atmosphérique.
En effet, le principe fondamental de l'hydrostatique fournit : \(P_{O}=P_{vide}+\rho_{Hg} \cdot g \cdot \left(h+H\right) = P_{atm} + \rho_{Hg} \cdot g \cdot h\).
On obtient ainsi la relation qui relie directement la différence de niveau \(H\) entre les deux branches donne la pression atmosphérique : \(P_{atm}=\rho_{Hg} \cdot g\cdot H\).
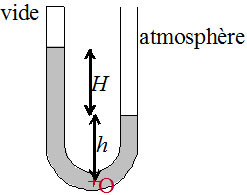
La plupart des baromètres à mercure sont conçus avec un réservoir dans la branche de droite, dans laquelle le niveau est par conséquent quasiment constant ; on lit alors la pression atmosphérique directement avec la hauteur de mercure dans la branche de gauche, qui peut être graduée en mmHg ou en "véritable" unité de pression.
Autres exemples d'applications
Exemple : Presse hydraulique
Impossible d'accéder à la ressource audio ou vidéo à l'adresse :
La ressource n'est plus disponible ou vous n'êtes pas autorisé à y accéder. Veuillez vérifier votre accès puis recharger le média.
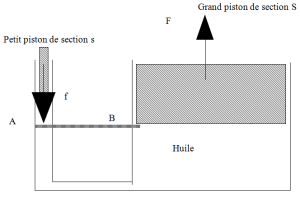
La presse hydraulique est un moyen simple de démultiplier les forces.
Le principe des vases communicants impose que la pression soit la même aux points A et B (tant que l'huile est immobile ou quasiment).
Or la force \(f\)[9] exercée sur le petit piston est telle que \(P_{A} = \frac{f}{s}\).
La force \(F\)[9] transmise au grand piston est quant à elle telle que \(P_{B} = \frac{F}{S}\) et comme \(P_{A} = P_{B}\), on a finalement :
\(F = f \cdot \frac{S}{s}\)
Ainsi la force transmise au grand piston est d'autant plus grande que le rapport des sections des pistons est grand : ce principe donne la possibilité de soulever de lourdes charges en B en appliquant une force \(f\) relativement petite en A.
Exemple : Barrage
Impossible d'accéder à la ressource audio ou vidéo à l'adresse :
La ressource n'est plus disponible ou vous n'êtes pas autorisé à y accéder. Veuillez vérifier votre accès puis recharger le média.
Exemple : Crève-tonneau de Pascal
Impossible d'accéder à la ressource audio ou vidéo à l'adresse :
La ressource n'est plus disponible ou vous n'êtes pas autorisé à y accéder. Veuillez vérifier votre accès puis recharger le média.
Poussée d'Archimède
Si on plonge un objet dans de l'eau, la pression de l'eau au bas de l'objet est plus grande que la pression en haut de l'objet d'après ce qu'on vient de voir. En effet, le bas de l'objet est plus profond, donc là où la pression est plus grande. Au final, l'objet subit donc une force dirigée vers le haut, exercée par l'eau. Cette force provient de la différence de pression entre le haut et le bas de l'objet. On l'appelle poussée d'Archimède.
Si cette force est plus grande que le poids de l'objet, il est poussé vers le haut, et reste à la surface : il flotte (c'est le cas d'un morceau de bois). Si cette force est plus petite que le poids de l'objet, c'est le poids qui l'emporte, et l'objet coule (exemple du caillou).
Imaginons un instant qu'à la place de notre objet, on ait de l'eau. L'eau à la place de l'objet n'aurait aucune raison de flotter ou de couler ; elle resterait sur place : son poids compenserait exactement la poussée d'Archimède. En résumé, l'objet subit exactement la même poussée d'Archimède que l'eau qu'on imaginait à sa place. Autrement dit : l'objet subit une poussée d'Archimède égale au poids de l'eau correspondant au volume occupé par l'objet, mais dirigée vers le haut.
On énonce généralement ceci sous la forme du principe d'Archimède : « tout corps plongé dans un liquide subit un poussée dirigée vers le haut égale au poids du liquide déplacé »
. En fait, ceci est vrai dans tout fluide (donc également dans les gaz).
Cette vidéo reprend et détaille l'explication ci-dessus.
Impossible d'accéder à la ressource audio ou vidéo à l'adresse :
La ressource n'est plus disponible ou vous n'êtes pas autorisé à y accéder. Veuillez vérifier votre accès puis recharger le média.
Attention : La poussée d'Archimède n'est pas une nouvelle force !
Comme on l'a vu, cette poussée d'Archimède n'est autre que la résultante des forces de pression qui s'exercent sur le corps. Il ne faut donc en aucun cas, lorsque l'on effectue un bilan de forces, vouloir prendre en compte à la fois la poussée d'Archimède et la résultante des forces de pression (on compterait deux fois la même force !).
Exemple : Densimètre
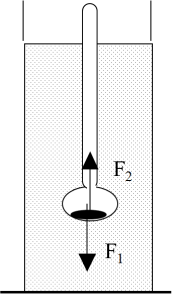
Si l'on reprend le bilan des forces qui s'exercent sur ce densimètre :
force de pesanteur \(F_{1} = m \cdot g\)
poussée d'Archimède \(F_{2} = \rho_{liq} \cdot g \cdot V_{immerg}\)
où \(m\) est la masse constante du densimètre et \(V_{immerg}\) son volume immergé (variable selon la position du densimètre).
À l'équilibre, \(F_{1} =F_{2}\), ce qui donne \(\rho_{liq} = \frac{m}{V_{immerg}}\).
Plus \(\rho_{liq}\) est grande, moins le volume immergé \(V_{immerg}\) est grand et plus le densimètre s'élève.
On peut effectuer une lecture directe de la densité du liquide sur la tige graduée surmontant le réservoir à l'interface liquide/air.
Conclusion
Impossible d'accéder à la ressource audio ou vidéo à l'adresse :
La ressource n'est plus disponible ou vous n'êtes pas autorisé à y accéder. Veuillez vérifier votre accès puis recharger le média.