HYDRAULIQUE pour le génie des procédés

On sait par expérience que lors d'une plongée en haute mer par exemple, plus le plongeur descend profond dans l'eau, plus la pression qu'il subit augmente. Pour le comprendre, on peut imaginer que le plongeur subit une force correspondant au poids d'eau au-dessus de lui : plus il descend profond, plus le poids d'eau au-dessus de lui est important. Il semble donc que la pression augmente avec la profondeur.

Réciproquement, on sait également par expérience que la pression diminue avec l'altitude. Ainsi l'opercule relativement souple d'un pot de yaourt acheté dans la vallée, "gonfle" quand le yaourt est emporté en haute montagne. On peut également citer la nécessité de pressuriser les cabines d'avion ou encore le mal d'altitude.

On se propose de démontrer approximativement ce principe.

On désignera par $x$^[3] et $y$^[4] les coordonnées dans le plan horizontal et $z$^[1] la coordonnée verticale (ou côte).

En décomposant les vecteurs, on peut également écrire cette relation :

• en coordonnées cartésiennes : $\left[ \begin{array}{r l}& \frac{\partial P}{\partial x} \\ \\& \frac{\partial P}{\partial y} \\ \\& \frac{\partial P}{\partial z} \end{array} \right] = \rho \cdot \left( \begin{array} {r l} & G_{x} \\& G_{y} \\& G_{z} \end{array} \right)$ ;

• en coordonnées cylindriques : $\left[ \begin{array}{r l}& \frac{\partial P}{\partial r} \\ \\& \frac{\partial P}{\partial \theta} \\ \\& \frac{\partial P}{\partial z} \end{array} \right] = \rho \cdot \left( \begin{array} {r l} & G_{r} \\& G_{\theta} \\& G_{z} \end{array} \right)$.

Dans le champ de pesanteur seul, $\frac{dP}{dz}=-\rho \cdot g$, où $g$^[6] est l'accélération de la pesanteur.

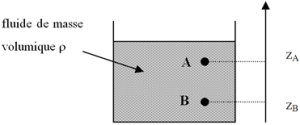
La différence de pression entre deux points A et B est obtenue en intégrant l'équation différentielle entre ces deux points : ${{P}_{A}}-{{P}_{B}}=\rho \cdot g\cdot \left( {{z}_{B}}-{{z}_{A}} \right)$

Ceci peut s'énoncer par le principe de Pascal : « La différence de pression entre 2 niveaux d'un fluide homogène au repos, est égale au poids de la colonne de fluide de section unitaire et de hauteur correspondant à la différence de cote des 2 niveaux. »

Le principe de Pascal peut donc s'énoncer ainsi : « Les fluides incompressibles transmettent les variations de pression. »

On peut signaler également la fameuse expérience du tonneau de Pascal illustrant la transmission des surpressions par un fluide. Un tonneau intégralement rempli d'eau est surmonté par un très long tube rigide de faible diamètre communiquant avec l'intérieur du tonneau. On remplit alors le tube avec de l'eau jusqu'à une hauteur $h$^[9] suffisamment importante pour que la pression régnant à l'intérieur du tonneau fasse éclater ce dernier.

En effet, $P_{int} = P_{atm} + \rho \cdot g \cdot h$.

À partir de l'équation ${P_{1}} + \rho \cdot g \cdot z_{1} = P_{2} + \rho \cdot g \cdot z_{2}$, on peut souligner quatre points :

1. dans un fluide incompressible en équilibre, les variations de pression se transmettent intégralement en tout point du fluide (c'est-à-dire que si la pression au point 1 augmente par exemple de 5 bar, la pression au point 2 augmentera également de 5 bar) ;

2. dans un fluide en équilibre, soumis seulement à la force de gravitation, la pression est uniforme en tout point d'un plan horizontal dans un même fluide (c'est-à-dire que si les points 1 et 2 sont situés à la même cote, il y régnera la même pression) ;

3. pour un fluide en équilibre statique isotherme, la différence de pression entre deux niveaux est égale au poids de la colonne de fluide entre ces deux niveaux ;

4. plus la masse volumique du fluide est grande et plus la pression est élevée (c'est-à-dire que pour une même pression $P_{1}$ au point de cote $z_{1}$, si on remplaçait le fluide par un autre, de masse volumique supérieure, la pression au point 2 -situé en dessous du point 1- sera supérieure à celle qui y régnait avec le fluide initial).